
 | Deutsch
| English
| Deutsch
| English
FED3+: Toleranz für LK0 bei Drehfedern mit und ohne Windungsabstand

In FED3+ wird für die Federkörperlänge LK0 der Schenkelfeder die Toleranz nach DIN 2194 für Drehfedern mit Windungsabstand berechnet und ausgegeben. Über die Toleranz für Drehfedern ohne Windungsabstand gibt es in der DIN keine Aussage, in FED3+ wird auch für a=0 die angegebene Formel verwendet. Wenn das Windungsverhältnis Dm/d allerdings größer als 10 wird, steigt die Toleranz exponentiell an. Bei Dm/d > 20 wird die Toleranz von LK0 größer als LK0 selber. Wenn Sie LK0 ohne Toleranz ausgeben wollen, gehen Sie unter Bearbeiten\Toleranz auf "andere.." und geben 0 ein. Neu für FED3+ gibt es jetzt auch einen Vorschlags-Button "<" wenn a=0 ist (ohne Windungsabstand). Dann wird eine Toleranz für LK0 vorgeschlagen nach der Formel:
A Lk0 (ohne Windungsabstand) = (n+1) * Ad + Adelta0 / 360° * d
Mit Ad=Toleranz Drahtdurchmesser, Adelta0=Toleranz Schenkelwinkel, n=Windungszahl, d=Drahtdurchmesser.
WN6: Quick3-Ansicht
Die neue Quick3-Ansicht enthält Zeichnungen und Tabellen mit Abmessungen und Festigkeit der P3G-Verbindung.

WN6: Einsatzmöglichkeit von P3G-Polygonprofilen
In der DIN 32711 steht, dass P3G-Profile nicht geeignet sind für unter Drehmoment längsverschiebbare Verbindungen. Wieso das so ist, steht davor als Vorteil: Selbstzentrierung von Welle und Nabe unter Drehmoment. Tatsächlich ist die Exzentrizität (e=Zahnhöhe/2) der DIN-Größen relativ klein, vermutlich wegen der Herstellbarkeit mit Polygonschleifmaschinen. Deshalb verklemmen sich Welle und Nabe bei Torsion. Bei wechselnder Last ist das nicht so gut: dann löst sich die Klemmung und verklemmt auf der anderen Seite. Gleitverschleiß, Aufweitung und Verdrehspiel sind die Folgen bei Drehrichtungsumkehr.
In WN6 kann man alle Abmessungen auch direkt eingeben und eine größere Exzentrizität eingeben, das mindert die Klemmung. Mit Polygonschleifmaschinen kann das Nabenprofil dann vielleicht nicht mehr hergestellt werden; nur noch als gezogenes Profil von der Stange und das Nabenprofil geräumt, gegossen, gespritzt, oder 3D-gedruckt.
Wenn man allerdings die Exzentrizität zu groß wählt, bekommt man den vom P4C-Profil bekannten Effekt, dass die Polygonkurve die harmonische Bahn verlässt. Dann muss man die Kurve wie beim P4C-Profil mit einem Kreisbogen begrenzen.
Die größtmögliche Exzentrizität für eine harmonische Kurve ist elim = d /16 = 0.0625*d1.
WN6: Datenbank erweitert bis 180 mm
Neue Größen 110mm bis 180mm nach DIN 32711-1:2009 wurden in die Datenbank p3g.dbf übernommen.

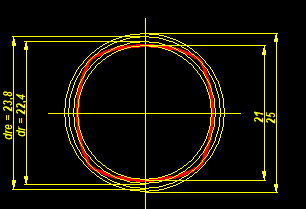
WN7 – Hilfebild
Für die Abmessungen in WN7 wurde das Hilfebild verbessert, ergänzt um ein Bild mit der kompletten Kontur und dem Durchmesser des konkaven Kreisbogens dre.

WN7: Quick3-Ansicht
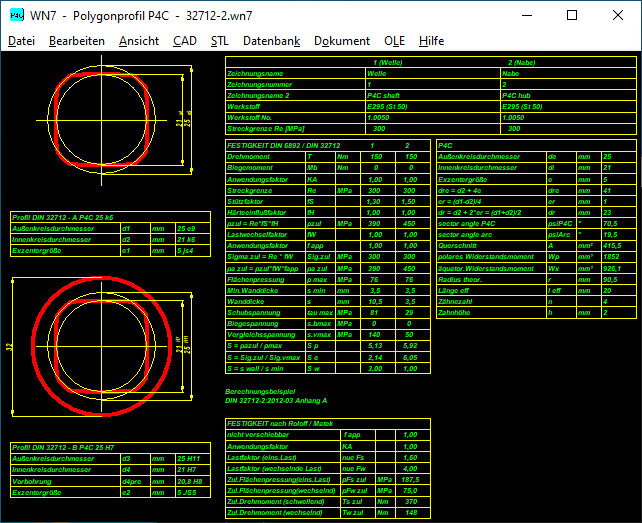
Die neue Quick3-Ansicht enthält Zeichnungen und Tabellen mit Abmessungen und Festigkeitsberechnung der P4C Verbindung.
WN7: P4C-Datenbank erweitert bis 180 mm
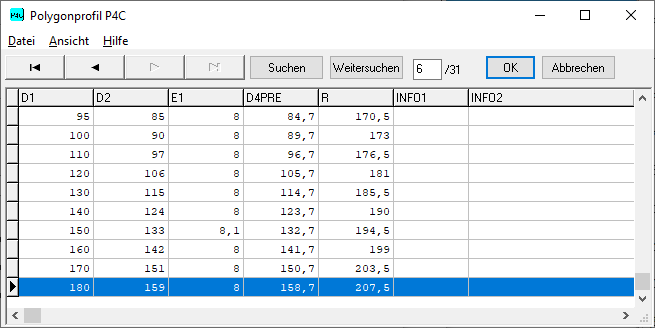
Neue Größen 110mm bis 180mm nach DIN 32712-1:2009 wurden in die Datenbank p4c.dbf übernommen.
WN7 – theoretischer Außenkreisdurchmesser "dre"
Für den (theoretischen) Außendurchmesser des durchgehenden Trochoidenprofils wird in WN7 die Bezeichnung "dre" eingeführt und mit ausgedruckt. In DIN 32712 gibt es schon einen ähnlichen Wert "dr" als mittleren Durchmesser für die Berechnung der Flächenpressung:
dr = d2 + 2e
dre = d2 + 4e
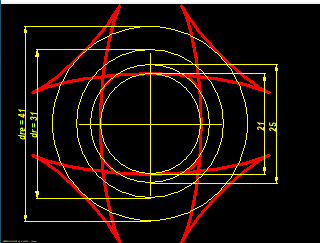

Profil DIN 32712 – P4C 25 mit d1=25mm, d2=21mm, e=5mm -> dre=d2+4e=41mm
Für selbst definierte Profile kann man d1, d2 und Exzentrizität e1 eingeben.
Wenn man den zylindrischen Anteil vergrößern will, kann man d1 verkleinern.

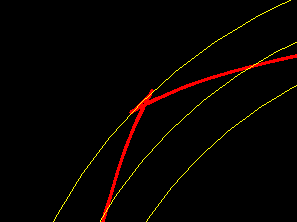
Wenn man "dre" = d1 setzt, dann wird die Exzentrizität e=(d1-d2)/4 = 1mm. Aber für ein harmonisches Profil ist die Exzentrizität noch zu groß.
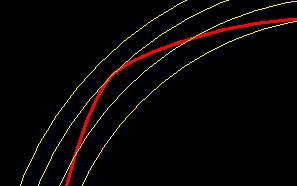
Erst wenn man die Exzentrizität weiter verkleinert auf 0.7mm, erhält man ein harmonisches "P4G" Profil. Der Außendurchmesser dre ist jetzt kleiner als der Durchmesser d1 der ursprünglichen DIN-Größe.
Für ein harmonisches PnG-Profil muss die Exzentrizität kleiner sein als rm/(n²-1). Für P4G e<= rm/15, mit rm=23/2 ist elim= 0.766 mm.
WN7 – P4C-Sektorwinkel berechnet

Das P4C-Gleichdick-Profil wird von einem Kreisbogen geschnitten. In der Quick3-Ansicht werden jetzt die anteiligen Winkel angezeigt: psiP4C mit Polygonprofil und psiarc mit Kreisbogen. Addiert ergeben die beiden Winkel 90 Grad.
P3G und P4C Normreihe
Weil in der Normreihe Durchmesser und Exzentrizität auf ganze Zahlen gerundet wurden, sieht jedes Profil anders aus. Vergleichen Sie ein P4C-Profil mit Nennmaß 14 und Nennmaß 100!
Dazu gibt es eine Publikation von Prof. Masoud Ziaei, der P3G und P4C Verbindungen untersuchte und daraus optimale Abmessungen ableitete:
P3G: Exzentrizität e = 0.036 * dm
P4C: Exzentrizität e = 0.125 * dm, d2/d1=0.82
Beim P4C ist dm=d2+2*e. Mit dm=d2+2*0.036dm wird dm=d2/0.928 und mit d2=0.82d1 wird
Dm=0.82d1/0.928 = 0.8836 d1. e=0.125*dm = 0.11*d1. Der Herr Professor behauptet jedoch, dass der Gleichdickdurchmesser auch für P4C nach DIN 32712 dm=d1 sei. Es bleibt demnach vorerst unklar, wie groß die optimale Exzentrizität für P4C nach Ziaei ist.
Die Benennungen d1 bis d6 in DIN 32711 und 32712 sind willkürlich benannt. Bei P3C ist die Nenngröße d1 der mittlere Durchmesser (Gleichdickdurchmesser), bei P4C nach DIN 32712 ist d1 der Außendurchmesser (welcher mit dem Polygon gar nichts zu tun hat).
GEO1+: Polygon Profil (P3G)
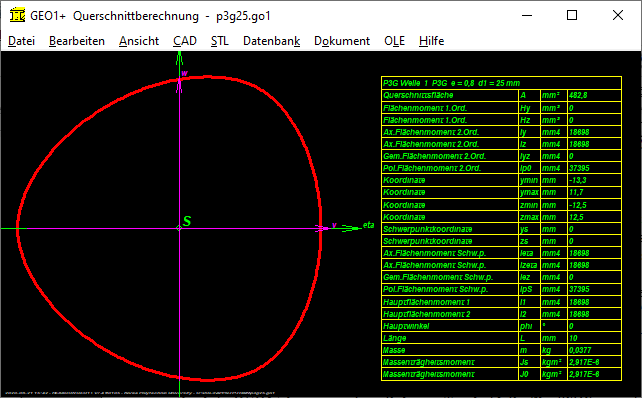
Auch in GEO1+ kann man jetzt Polygon-Trochoid-Profile (P3G) generieren. Hier kann man außer Teilkreisdurchmesser und Exzentrizität noch die Anzahl der Ecken sowie die Auflösung eingeben.
Ein Polygon-Trochoid mit 2 Ecken ergibt eine Ellipse. Mit 3 Ecken ein P3G Profil. Mit 4 Ecken ergibt sich eine P4C Kontur, aber ohne Begrenzung durch Kreisbogen. Eine richtige P4C-Kontur kann man aber auch in GEO1+ laden: in WN7 unter "Datei\Export DXF" bzw. "CAD\P4C" speichern, dann in GEO1+ unter "Datei\Import DXF" laden. In GEO1+ werden Fläche und Flächenmomente aus der Summe der Koordinaten berechnet. Ein Vergleich eines in GEO1+ generierten P3G Profils mit berechneten Daten aus WN6 ergibt eine gute Übereinstimmung bei Querschnittsfläche A und Flächenmomenten Ip und Ix. Der Schwerpunkt liegt genau im Nullpunkt. Das Widerstandsmoment Wmin ist I/rmax mit rmax=d2/2. Bei Wx=Ix/d2/2 gibt es eine gute Übereinstimmung, bei Wp=Ip/d2/2 gibt es eine Abweichung von ca. 10% mit Wp aus DIN 32711.
Mit GEO1+ kann man auch das Massenträgheitsmoment einer Welle mit P3G-Profil ermitteln.
WN7: Zwei Fehler in DIN 32712

Ein DXF-importiertes P4C Profil aus WN7 ergibt in GEO1+ für Wp einen höheren und für Wx einen niedrigeren Wert als nach DIN 32712.
Das lässt sich dadurch erklären wie das Widerstandsmoment nach DIN 32712 berechnet oder besser gesagt geschätzt wird:
Wp = 0.2 * d2³
Wx = 0.15 * d2³
d2 ist der kleinste Durchmesser am P4C-Profil. Das Widerstandsmoment eines P4C-Profils ist also auf jeden Fall größer als das einer Welle mit Durchmesser d2:
Wp = pi/16 (0.196) * d2³
Wx = pi/32 (0.098) * d2³
Das polare Widerstandsmoment eines P4C-Profils ist nach DIN 32712 konservativ berechnet, aber das axiale Widerstandsmoment Wx wird zu groß berechnet. Also Vorsicht, wenn eine P4C-Welle auf Biegung beansprucht wird! P4C-Kontur in WN7 als DXF-Datei speichern und mit GEO1+ laden. GEO1+ berechnet dann das axiale Flächenmoment 2.Ordnung Iz. Wenn die P4C-Welle auf der Gleichdick-Kontur aufliegt, ist Wx = Ix/(d2/2). Wenn die P4C-Welle auf der Kreiskontur aufliegt, ist Wx = Ix/(d1/2).
In WN7 wurde die näherungsweise Berechnung von Wx abweichend von DIN 32712 geändert in Wx = 0.1 * d2³
Einen noch gravierenderen Fehler gibt es bei der Berechnung der Flächenpressung nach DIN 32712 Beweis: Exzentrizität sehr groß machen (für flache Kurve), dann geht die Flächenpressung p gegen 0. Weil dr=d2+2e angegeben ist. Anders als bei P3G kann man bei P4C die Exzentrizität beliebig groß machen (Exzentrizität unendlich ergibt Polygon geschnitten mit Kreis). Vermutlich sollte dr=d2+2er sein. Weil dr der mittlere Durchmesser dm=Rm/2 sein soll (äquivalent zu d1 bei P3G) dr=(d1+d2)/2 = d2+2*er = d1-2*er. In WN7 wird zukünftig abweichend von der DIN 32712 mit "dr = d2 + 2*er" statt mit "dr=d2+2*e" gerechnet.
Angewendet auf das Berechnungsbeispiel in DIN 32712-2:2012 Anhang A ist dr dann 23mm statt 31mm, dadurch wird die Flächenpressung p = 80 MPa statt 51,57 MPa.
Eine Alternativberechnung p=F/A mit F=Mt/(dm/2) und Fläche A=Zahnhöhe*Breite*Zähnezahl ergibt sogar einen noch höheren Wert von 94 N/mm². Fast doppelt so groß wie nach DIN!
WN6: Fehler in DIN 32711
Auch in DIN 32711 gibt es einen kleinen Fehler: die recht komplizierte Formel für die Berechnung des polaren Widerstandsmoments Wp ist falsch. Beweis: Exzentrizität e=0 setzen, dann müssen die Werte von Ip, Wp, Wx, A mit den Werten eines Kreisquerschnitts übereinstimmen.
Richtiger wäre die einfache Formel Wp = 2*Ip/d1
Die Abweichung ist nicht gravierend, deshalb wird die DIN-Berechnung in WN6 vorerst beibehalten. Zusätzlich wird das Widerstandsmoment "Wpd1 = 2*Ip/d1" berechnet und mit ausgedruckt.
Das Widerstandsmoment des P3G-Profils wird sowieso nur für die Berechnung der Schub- und Biegespannung von Vollwellen verwendet. Für Nabe oder Hohlwelle wird das Widerstandsmoment eines Kreisrings verwendet.
Auch die Berechnung der Mindestwanddicke nach DIN 32711 und 32712 ist zumindest fragwürdig. Für P3G-Verbindungen ist die Mindestwanddicke doppelt so groß wie für P4C-Verbindungen.
Vielleicht wird angenommen, dass P3G für Preßverbände und P4C für verschiebbare Verbindungen verwendet werden.
Neue Software für PnG Verbindungen
Demnächst gibt es ein neues Berechnungsprogramm WN13 für PnG-Verbindungen mit 2, 3, 4, 5, 6, n Ecken (P2G, P3G, P4G, P5G, PnG) wobei man Gleichdickdurchmesser und Exzentrizität frei eingeben kann. Die maximale Exzentrizität ist elim = d / (2*(n²-1)). Polygonwellenverbindungen könnten die bevorzugte Welle-Nabe-Verbindung für spanlos hergestellte Maschinenelemente werden.

Neue Software für PnC Verbindungen
Demnächst gibt es auch ein neues Berechnungsprogramm WN14 für PnC-Verbindungen mit abgeschnittenem Polygon-Trochoid-Profil wie P4C, aber auch mit 2,3,5,6 Ecken.
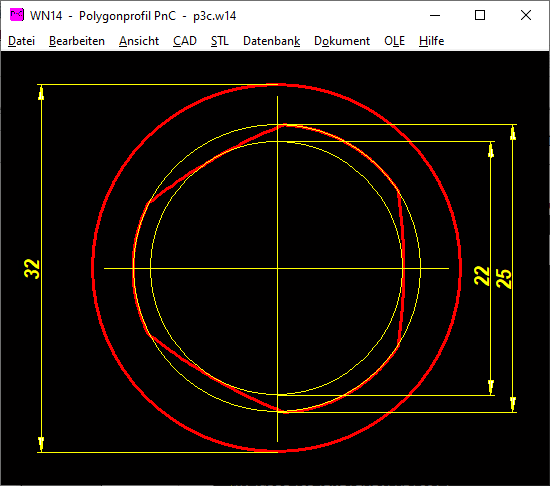
Das PnC-Profil ist auch interessant für Wellen, die sowohl zylindrische als auch PnC Maschinenelemente aufnehmen können, z.B. Wälzlager, Zahnräder und Riemenscheiben auf einer durchgehenden Welle.
TR1: Polygon-Trochoid Profil (P3G)
In die Profil-Datenbank zur Trägerberechnung wurde die Polygontrochoidwelle aufgenommen. Damit können Wellen mit P3G-Profil als Träger berechnet werden. Allerdings nur auf Zug/Druck und Biegung, nicht auf Torsion. Die Anzahl der Ecken kann eingegeben werden. Bei 2 Ecken gibt es eine Ellipse. Je mehr Ecken, desto kleiner muss die Exzentrizität sein. Sonst gibt es den bei P4C-Profilen bekannten Effekt, das nutzbare Profil mittels Kreisbogen zu begrenzen.

Auch in TR1 gibt es darüber hinaus die Möglichkeit, beliebige aus einer Polylinie bestehende Querschnitte als DXF-Datei zu importieren.
Unter "Ansicht \ Profil mit Spannung und Biegung" wird die Biegespannung in jedem Punkt des Profils angezeigt, außerdem die Durchbiegung an der angegebenen x-Koordinate (gelbe Kontur).

GEO4: Import DXF
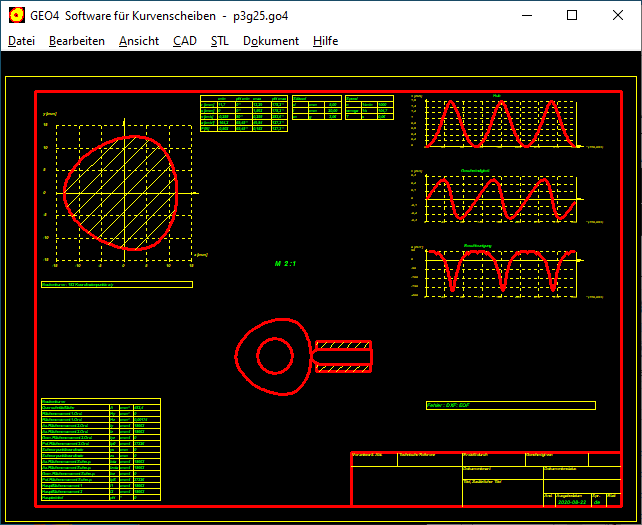
Über die DXF Importfunktion kann man Polygonprofile aus WN6 oder GEO1+ in GEO4 für eine P3G-Nockenform übernehmen.
ZAR4: Import DXF
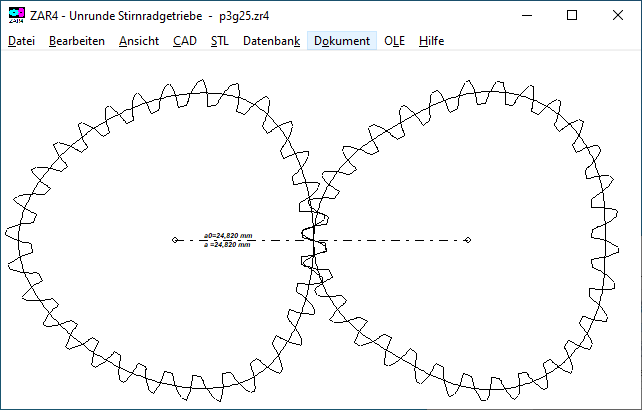
Über die DXF Importfunktion kann man Polygonprofile aus WN6 oder GEO1+ in ZAR4 als P3G-Zahnrad übernehmen.
ZAR1+, ZARXP, ZAR1W, ZAR5, ZAR7, ZAR8: Fussausrundungstrochoide bei Unterschnitt

Für sehr stark unterschnittene Zahnräder (z.B. alfa=15° und x=-1.3) war die Fußausrundungstrochoide am Übergang zur Evolvente nicht sauber gezeichnet worden. Bei diesem ungewöhnlichen Zahnrad liegt der Teilkreisdurchmesser außerhalb der Verzahnung, und der Unterschnittbereich mit der Fußausrundung ist größer als die Evolvente. Auch solche Verzahnungen werden jetzt durchgängig gezeichnet, wenn man zuvor unter "CAD\Einstellungen\Fussausrundung zeichnen" den Startwinkel der Fussausrundung vergrößert (+2pi statt +0pi).


ZAR1+, ZAR5, ZAR7, ZAR8: Bohrung P3G, P4C, P4G, P3C, P6G, Viereck, Sechseck
Für die Herstellung von Zahnrädern mit 3D-Drucker gibt es zu einer runden Bohrung jetzt verschiedene Alternativen:


Angeflacht, 4-kant, 6-kant, P3G, P4C, P4G, P6G, P3C. Außerdem noch eine Paßfedernut und eine Sinuswelle. Man muss keine weiteren Abmessungen eingeben, es werden Standardwerte verwendet. Beim P3G ist d1=dB, e2=0.04 dB (d5=dB+e2, d6=dB-e2)

Unter "CAD\Zahnräder" kann man die Optionen wählen und eingeben:
Außer P3G und P4C gibt es auch P3C, P4G, P6G, und runde Sinuswelle.



ZAR1+ 3+ 4 5 7 8: Zahnräder mit 3D-Drucker herstellen
Geradverzahnte Zahnräder kann man leicht im 3D-Druck herstellen. Bei schrägverzahnten Zahnrädern sollten danach die Zahnflanken geglättet werden, weil im 3D-Druck die Zahnschräge eine Treppenfuntion ergibt (Stufenhöhe=Schichtdicke).
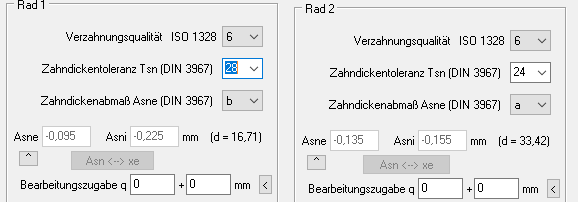
Wegen der größeren Toleranzen bei 3D-Druck von Zahnrädern aus PLA oder ABS muss das Flankenspiel vergrößert werden, so dass die Modellzahnräder auch laufen. Unter "Bearbeiten\Qualität" wählen Sie ein Toleranzfeld für großes Flankenspiel, z.B. b 28 für Zahnräder aus PLA oder ABS. Keine Bearbeitungszugabe (0).
Um die Druckzeit zu verkürzen, können Sie den Bohrungsdurchmesser vergrößern.
Bei schrägverzahnten Zahnrädern sollten Sie unter "Datei\Einstellungen\CAD" die Schichtdicke "zslice" konfigurieren. Diese sollte gleich sein wie die am 3D-Drucker eingestellte Schichtdicke.

Achtung: nicht unnötig klein einstellen, Halbierung von zslice verdoppelt die STL-Dateigröße.
Menü "STL Zahnrad":

Evolvente als Polylinie: egal, ob Polyline oder Line.
Durchmesser einzeichnen: nein, in die STL-Datei gehört nur die Zahnradkontur
Fußausrundung zeichnen: ja, wie in Zeichnungsdarstellung
Bohrung einzeichnen: ja, sonst kommt das Zahnrad auf Vollwelle
Auflösung Fußausrundung und Evolvente: wie in Zeichnungsdarstellung
Erzeugungsprofilverschiebungsfaktor: "<" Button für Toleranzmitte oder "min" "max" mit direkter Auswirkung auf das Flankenspiel.
Lochkreis: einen Lochkreis mit Bohrungen kann man für die Befestigung von Zahnrad oder Hohlrad verwenden, oder um einfach Material zu sparen.

Zahnstange: Für eine Zahnstange gibt man eine große Zähnezahl (-2000) und ein kleines Flankenspiel (unabhängig vom Teilkreis) ein, dann unter "STL\Sector\Rad2" Anzahl der Zähne eingeben.
ZAR1+ 5 7 8: Vorschlagswerte für Meßzähnezahl und Meßkreisdurchmesser
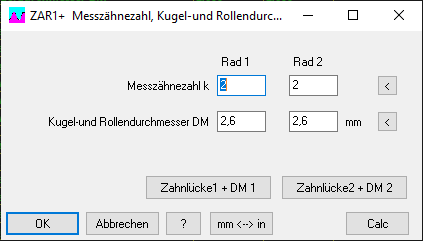
Die Vorschlagswerte mit "<" Button wurden aus dem Profilverschiebungsfaktor xemin berechnet, überprüft wurden die Eingabewerte dagegen mit Toleranzmitte (xemin+xemax)/2. Bei großen Zahnflankentoleranzen ergeben die Vorschlagswerte für den Größtwert von xe andere Meßzähnezahlen und Kugeldurchmesser als für den Kleinstwert mit mehr als 30% Unterschied. Für einige Grenzfälle ergab sich deshalb der kuriose Fall, dass eine Warnung "k measure !" angezeigt wurde, obwohl der Vorschlagswert verwendet wurde. Jetzt wird für alle Vorschlagswerte der aus den Zahndickenabmaßen berechnete mittlere Profilverschiebungsfaktor verwendet. Für den Hinweis danke ich Jong-Gak Kim von Pion.
Fehlalarm durch Virenscanner
Manche Virenscanner (für Computerviren) melden Warnungen für ausführbare Dateien, welche sie noch nicht kennen. Oder welche sie schon kennen, die sich aber geringfügig unterscheiden. Das trifft auf jede ausführbare Datei von HEXAGON zu: Jede exe-Datei ist anders und individuell, weil sie den Namen des Lizenznehmers enthält. Bei den meisten Softwareanbietern ist das anders, jeder Kunde arbeitet mit derselben exe-Datei. Das macht es Virenfirmen wie Symantec einfach, die Dateien zu katalogisieren, und dann einfach die exe-Datei mit den gespeicherten Merkmalen zu vergleichen: Wenn es Abweichungen gibt, könnte es sich um eine durch Computerviren mutierte Datei handeln. Bei HEXAGON Software gibt es immer Abweichungen: jede wfed1.exe ist anders. Das ist für Virenscanner verdächtig: sie finden zwar kein Virus, aber sie stellen eine vermeintlich mutierte Datei fest und geben eine Warnung aus. Bei Symantec heißt die Warnung "WS.Reputation.1". Diese Warnung können Sie ignorieren.
Corona-Viren auf Weltreise
Ein Virus kommt ohne fremde Hilfe keine zwei Meter weit. Viren werden durch Reisende übertragen. Corona-Viren reisen um die Welt. Im Frühjahr haben sie sich von Europa nach Südamerika verabschiedet, wo im Sommer Winter ist. Weiter über Nordamerika und Russland kehren sie zur Grippesaison zurück nach Europa. Nur nach China kommen die Viren nicht zurück: China hat alle internationalen Flüge bis auf Frachtflüge und einige wenige Heimkehrflüge für chinesische Überseestudenten gestrichen und alle Grenzen geschlossen, daß Reisende nicht die Corona-Pandemie zurückbringen. Freie Fahrt für Waren, dagegen Einreisestopp für Menschen und Tiere. Mit Erfolg: im Riesenreich China gibt es im August 2020 weniger Coronavirus-Neuinfektionen als im kleinen Freistaat Bayern. Wurden vor 6 Monaten Corona-Erkrankte erfolgreich isoliert, werden jetzt die Gesunden isoliert. Während andere Länder Milliarden für Corona-Folgen aufwenden, wird für China auch 2020 ein Wirtschaftswachstum erwartet.
In China braucht man keine Maske mehr. Die können alle in den Export. Nach Europa, dort sitzen die neuen Masken-Eiferer. Dort muss sogar ein EU-Kommissar zurücktreten, weil er einmal seine Maske vergessen hat.
Noch eine aktuelle Zahl vom Flughafen Stuttgart: Am 30.8.2020 gab es 72 Abflüge. Davon gingen 27 in Corona-Risikogebiete. Im Corona-Testzentrum am Flughafen werden täglich ca. 2000 Reiserückkehrer getestet. Davon seien im Durchschnitt 3% positiv. Drei Prozent, das sind 3.000 von 100.000.