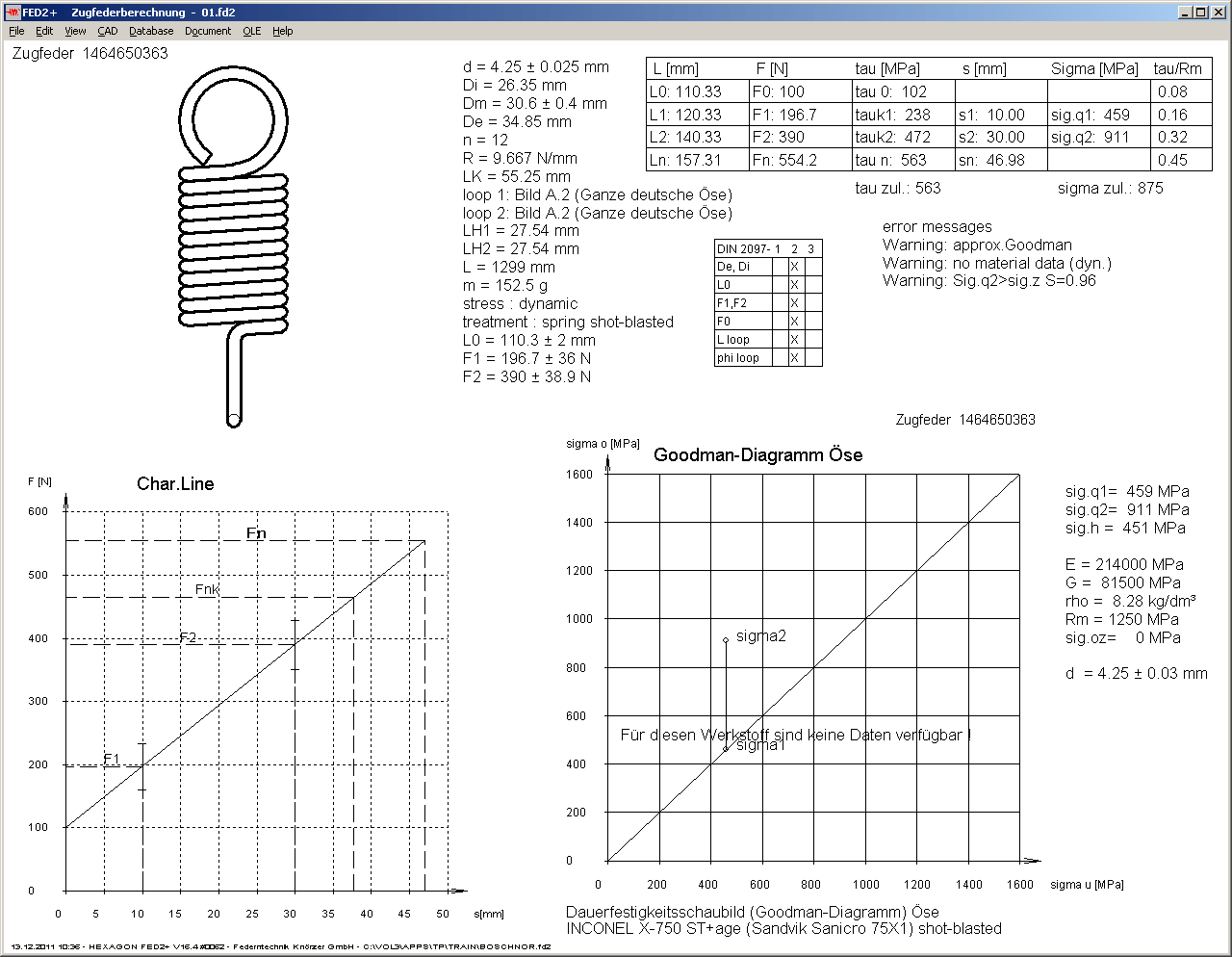
FED1+ Drahtlänge und Gewicht
Normalerweise wird die Drahtlänge einer Druckfeder genügend genau berechnet mit Ld = pi * Dm * nt. Die Federsteigung wird nicht berücksichtigt, und kann im Normalfall auch vernachlässigt werden. Nur bei Druckfedern mit sehr großer Steigung ergeben sich spürbare Abweichungen bei Drahtlänge und demzufolge auch dem Gewicht der Feder. In FED1+ wird die Drahtlänge nun nach einer genaueren Formel berechnet:
Ld = hypot(pi*Dm,P)*n + hypot(pi*Dm,d)*nE
Mit Dm=mittlerer Windungsdurchmesser, P=Steigung, n=Anzahl aktiver Windungen, nE=Anzahl Endwindungen, hypot=Hypotenusenfunktion c=sqrt(a²+b²)
FED2+ Nachrechnung bei Windungsabstand a>0
Wenn zwischen den Windungen ein Abstand a definiert wurde, waren in der Nachrechnung die Windungszahl n und Federkörperlänge bei Eingabe verändert worden. Der Fehler wurde korrigiert. Auch eine gelegentliche Veränderung von Daten bei Eingabe der Windungszahl (Ösenwinkel phi 360° statt 0° und n um 1 erhöht) wird durch Rundung des Ösenwinkels vermieden.
FED2+ Quick3
In der Quick3-Ansicht gab es manchmal Probleme, wenn für den Werkstoff keine Dauerfestigkeitsdaten vorlagen, jedoch Anwendung "dynamisch" definiert war. Hier wird nun ein leeres Goodman-Diagramm angezeigt.

FED2+ Selbstdefinierte Ösen
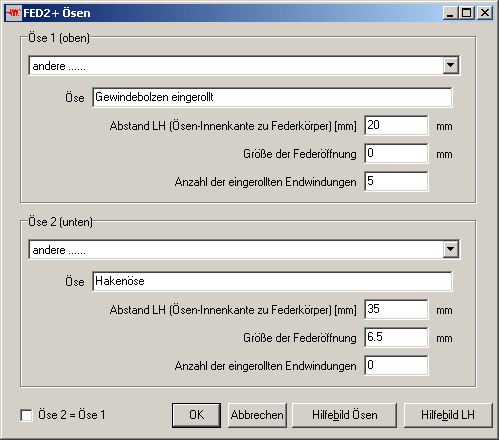
Bei der Berechnung von Drahtlänge und Ösenspannung wird unterschieden zwischen Ösen als Teil der Feder und eingerollten oder eingeschraubten Ösen oder Laschen (Bild A.9 bis A.12). Selbstdefinierte Ösen wurden bisher als eingerollte Ösen berechnet. Das wurde jetzt geändert: wenn die Anzahl eingerollter Endwindungen 0 ist, wird die Öse als Teil der Feder berechnet, ansonsten als externe Öse. Bei externen Ösen wird in der neuen Version außerdem die Drahtlänge genauer berechnet.
FED3+ Federpaketlänge LK alpha für Windungsabstand a > 0
Wenn die Federwindungen einer Schenkelfeder anliegen, wird die Federpaketlänge beim Einfedern etwas größer (bei Beanspruchung in Windungsrichtung). Wenn die Schenkelfeder mit Windungsabstand gewickelt ist (a>0), verändert sich die Federpaketlänge abhängig von Anwendung und Aufnahme der Schenkelfeder. In FED3+ kann man jetzt konfigurieren (unter Bearbeiten->Berechnungsmethode), wie LK alpha berechnet werden soll.

WN2, WN4, WN5 - Vergleich Toleranzsystem
In ISO 4156, ANSI B92.1 und ANSI B92.2M ist die Innenverzahnung der Nabe fest als Toleranzfeld "H" definiert, das Flankenspiel wird also vom Toleranzfeld der Wellenverzahnung (external spline) bestimmt. Bei Passverzahnungen nach DIN 5480 hat man hier größere Gestaltungsmöglichkeiten. Allen Normen gemein sind die Bezeichnungen "actual" und "effective" bezüglich der Berücksichtigung von Form-, Winkel- und Teilungsabweichung in den Zahndickentoleranzen. Leider unterscheiden sich die anderen Bezeichnungen der verschiedenen Normen recht stark, aber anhand der Toleranz-Schaubilder in WN2, WN5, und jetzt auch WN4, hat man nun eine gute Vergleichsmöglichkeit.
WN2+ Erweiterte Passungsauswahl für Zahnnabe
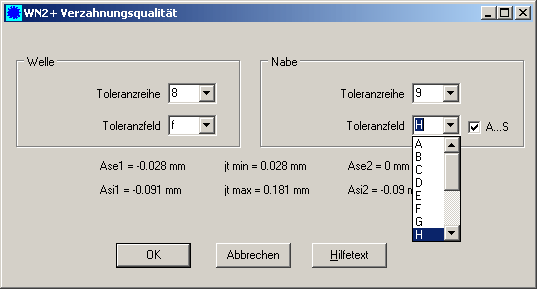
Nach DIN 5480 gibt es für die Zahnwelle die Toleranzfelder a bis v zur Auswahl, für die Zahnnabe dagegen nur die Toleranzfelder F,G,H,J,K,M. In WN2+ kann man jetzt für die Zahnnabe weitere Toleranzfelder von A bis S wählen, wenn man zuvor das Kästchen "A..S" anklickt.
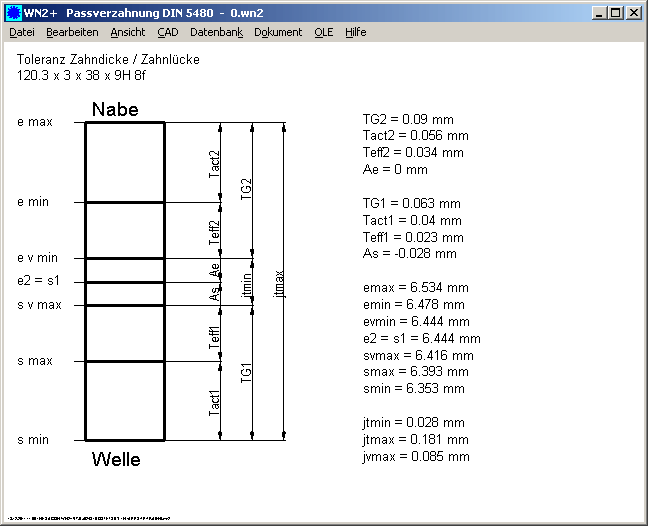
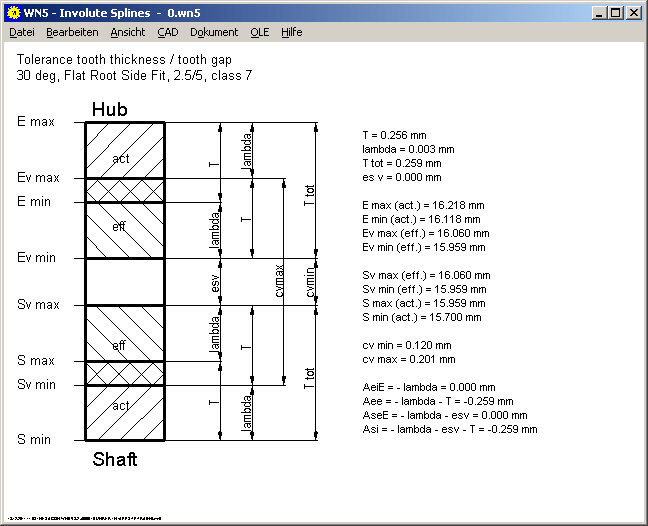
WN5 – Toleranzschaubild
Im Toleranzschaubild wurden Evmax und Svmin mit eingezeichnet. Außerdem werden die Toleranzzonen "actual" und "effective" schraffiert dargestellt. Neu ist auch die Anzeige der Abmaße Ase, Asi, Aee, Aei und ihre Berechnung. Das Größtspiel cvmax wird jetzt eingezeichnet als Evmax - Svmin (nicht mehr Emax – Smin).
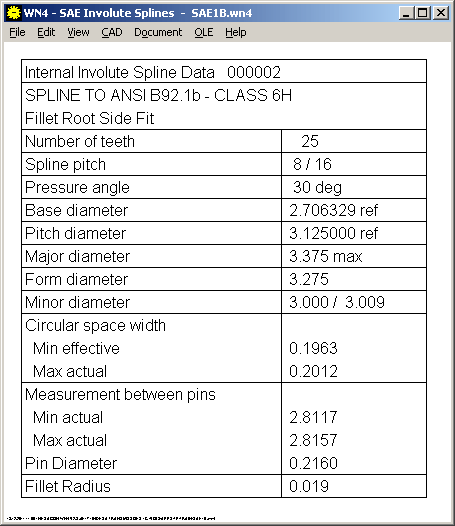
WN4 - Toleranzschaubild
In WN4 gibt es jetzt auch ein Toleranzschaubild wie in WN5 und WN2. Da die Bezeichnungen in DIN 5480, ANSI B92.1, ANSI B92.2M und ISO 4156 überall unterschiedlich sind, erleichtert dies den Vergleich der verschiedenen Toleranzsysteme und Bezeichnungen.

In den Tabellen mit Verzahnungsdaten wird nun das Rollenmaß "act" statt "eff" ausgegeben.
WN2, WN4, WN5: Drehflankenspiel jt und jv
Zusätzlich zum theoretischen Flankenspiel jtmin und jtmax wird das maximale effektive Flankenspiel jvmax in mm, sowie das entsprechende Drehflankenspiel in Winkelgrad ausgegeben. Für die maximale Verdrehung von Nabe und Welle ist das effektive Flankenspiel ausschlaggebend, da aufgrund von Form-, Winkel- und Teilungsabweichung die maximale Verdrehung der gesamten Paßverzahnung wesentlich geringer ist als das zulässige Flankenspiel eines einzelnen Zahns.
