FED1+ Wire Length and Spring Weight for High-pitch Springs
Until now, wire length was calculated Ld = pi * Dm * nt. Coil pitch was not considered, and can be neglected in most cases. Only springs with large pitch differ measurably on wire length and weight. Therefore, FED1+ uses a more precise formula now which includes pitch influence:
Ld = hypot(pi*Dm,P)*n + hypot(pi*Dm,d)*nE
With Dm = central coil diameter, P = pitch, n = number of active coils, nE = number of end coils, hypot = hypotenuse function c=sqrt(a²+b²)
FED2+ Recalculation of Extension Springs with Coil Distance a>0
If a wire distance "a" between coils was defined, number of coils n and spring body length LK was modified when entering spring dimensions at "Edit->Recalculation". The bug was fixed now.
FED2+ Quick3
Quick3 View of FED2 made sometimes problems, if "dynamic" application was defined, but no fatigue strength data for the Goodman diagram were available for the selected material. Now, FED2+ shows an empty Goodman diagram for this case.

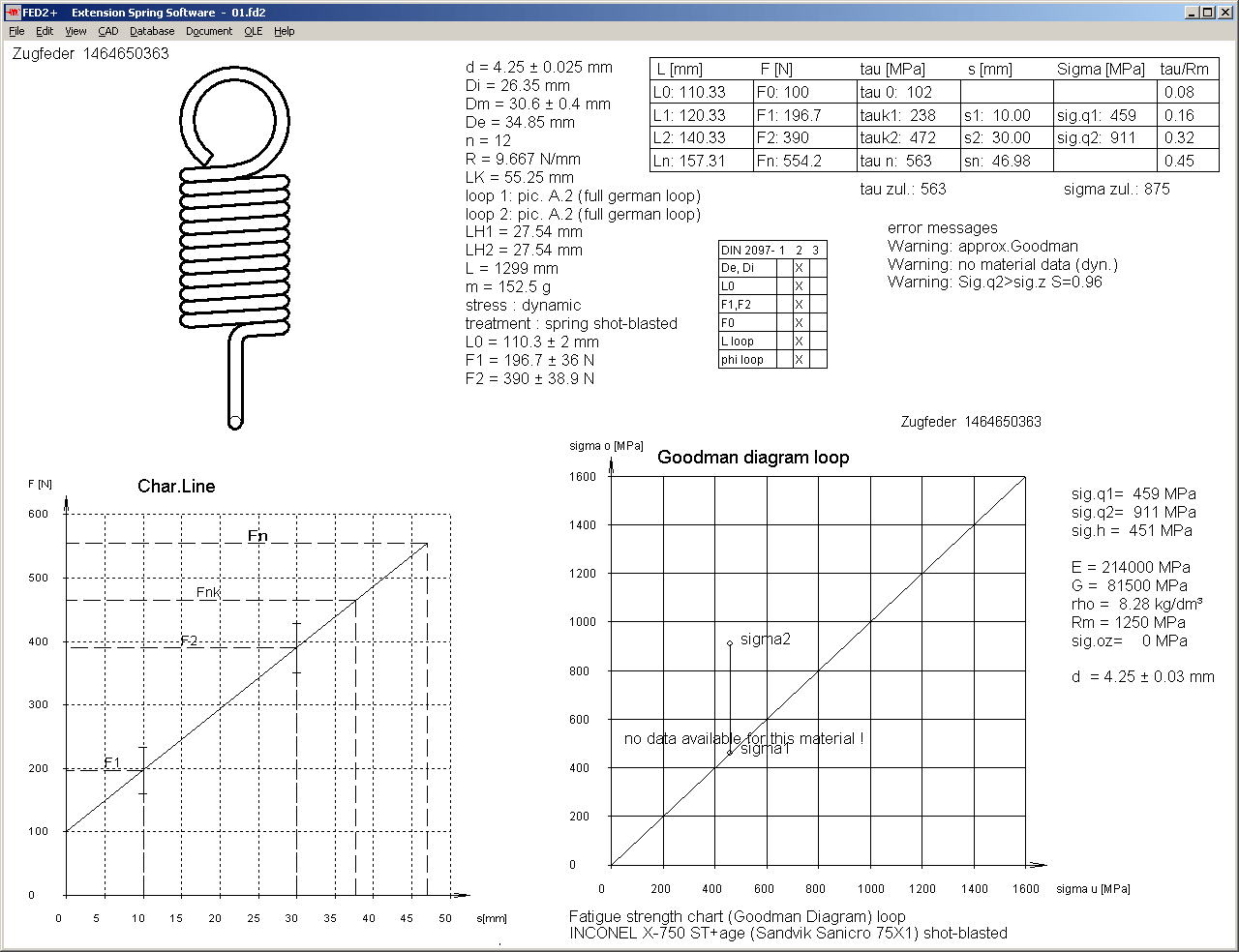
FED2+ Self-Defined Loops
Calculation of wire length and loop stress is distinguished by loops as part of the spring, and screwed-in external loops or bolts (picture A.9 .. A.12). Self-defined loops were calculated as external loops until now. This was changed now: if number of coils is 0, loop will be calculated like a hook loop, else it will be calculated as external loop. Furthermore, wire length is calculated more precise for external loops in the new version.
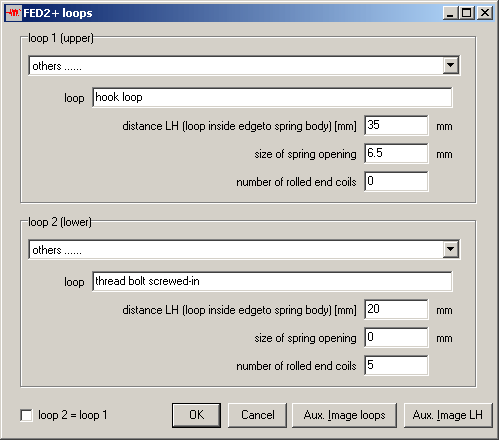
FED3+ Spring Body Length LK alpha for Coil Distance a > 0
Spring body length LK of torsion springs (a=0) increases on spring travel (load in coiling direction). If the torsion spring was coiled with distance between coils (a>0), variation of spring body length LK depends on application and bedding of the spring. In FED3+, you now can configure 3 possible variations of LK alpha:
WN2, WN4, WN5 - Comparison of Tolerance System
In ISO 4156, ANSI B92.1 and ANSI B92.2M, internal spline of the hub is defined fixed as tolerance zone "H", flank clearance is determined by the tolerance zone of the external spline (shaft). When designing involute splines according to DIN 5480 with WN2, you can vary tolerance zone of both, internal spline and external spline. Common to all standards are the terms "actual" and "effective" considering variation allowances in the flank clearance tolerances. Unfortunately, designation of the other terms are completely different, but by means of the tolerance charts in WN2+, WN5, and also in WN4 now, you have a clear comparison.
WN2+ Extended Selection of Fits for Internal Spline

According to DIN 5480, you can select tolerance zone "a" until "v" for the external spline, and tolerance zone "F,G,H,J,K,M" for the internal spline.. In WN2+, you now can select additional tolerance zones "A" until "S", if you check "A..S".
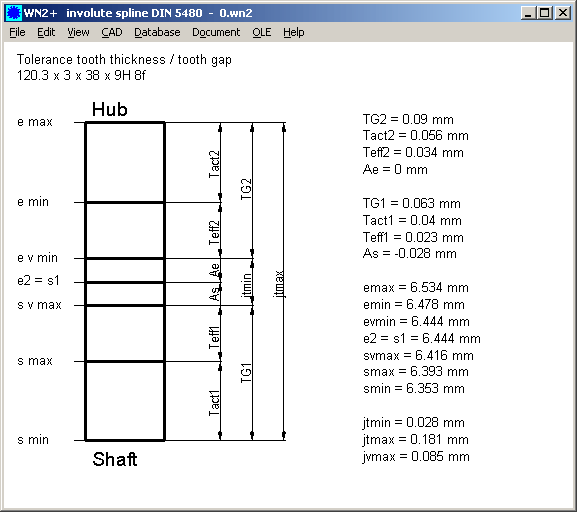
WN5 – Tolerance Chart
Evmax and Svmin have been added to the tolerance chart, and tolerance areas "actual" and "effective" are hatched now. Tolerances Ase, Asi, Aee, Aei have been added. Maximum clearance cvmav is now defined as Evmax - Svmin (not Emax – Smin).

WN4 - Tolerance Chart
WN4 now provides a tolerance chart like in WN5 and WN2+. This eases comparison of DIN 5480, ANSI B92.1, ANSI B92.2M and ISO 4156 with its different tolerance systems and designations.
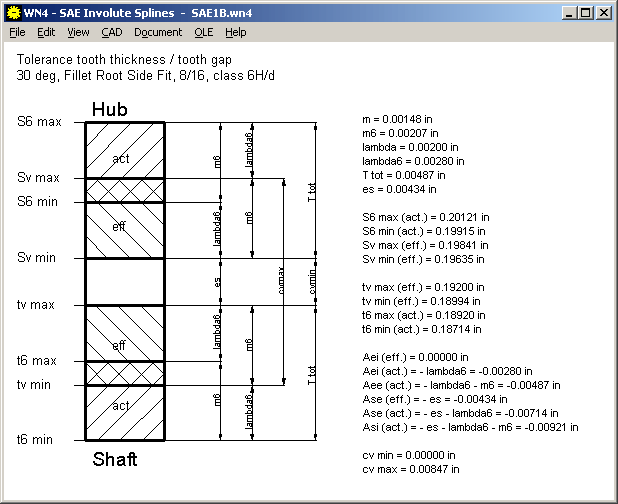
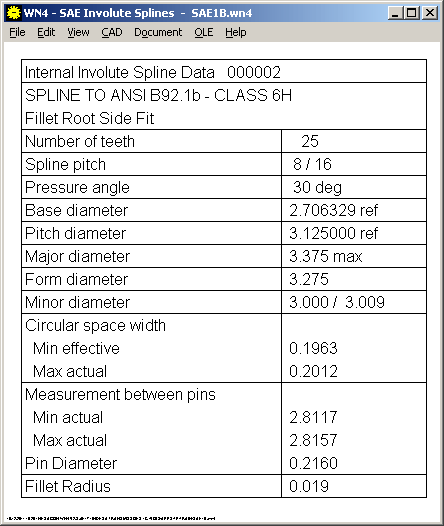
Tables with spline data now list the measurement over/between pins "act" instead of "eff".
WN2, WN4, WN5: Torsional Backlash jt and jv
Theoretical torsional backlash jtmin and jtmax, maximum effective backlash jvmax in mm, as well as corresponding torsional backlash jtmin, jtmax, jvmax in angular degree are listed in the printout now.
