 | English
| VDI 2230-1:2014
| English
| VDI 2230-1:2014
Die im November 2015 erschienene Ausgabe der VDI 2230 ist fast identisch mit der Ausgabe vom Dezember 2014. Eine Liste der Änderungen gegenüber der Ausgabe 2014 konnte ich nicht finden. So habe ich anhand meiner eigenen Fehlerliste überprüft, was korrigiert wurde.
Änderungen und Korrekturen in VDI 2230-1:2015
S. 36 (R9): Berechnung von SigmaSab nach Gleichung (188)
S. 102: Gleichung (211): "RS3" geändert in "RS" .
S. 102: Gleichung (213) .. + 1,2 * P für mzu geändert in 2 * P.
S. 122: Tabelle A9: 42CrMo4: pG = 300 N/mm² in 1300 N/mm² geändert.
S. 122: Tabelle A9: GJL-250 Wst-Nr. 0.6020 in 0.6025 geändert.
S. 132: Beispiel 1: R2: Mindestklemmkraft von 103 N in 10³ N geändert.
S. 134: Beispiel 1: R8: FSmax von 64 194 N in 66 194 N geändert.
S. 155: Beispiel 4, R8: .. "nach Gleichung (178)" in .. "nach Gleichung (163)" geändert.
S. 170: Beispiel 5: R11: mvorheff in meffvorh geändert.
VDI 2230-1:2015 - Verbleibende Fehler und Anmerkungen
S. 11: I, IB, Ibers, IBT ..
Übersetzungsfehler: Flächenträgheitsmoment = area moment of inertia (gyration=Rotation)
S. 35 (R8/1):
Zitat: FSmax = FMzul + phi en * FA max - deltaFVth
Besser: FSmax = max (FMzul, FVmax + FSAmax - deltaFVth)
Im Betriebszustand ist die Höchstlast FSmax = FVmax + FSAmax - deltaFVth
Bei der Montage ist die Höchstlast FSmax = FMzul.
S. 36 (R9/1):
Relevanter Querschnitt für Sigma a ist A0 statt AS bei Dehnschaftschrauben und Hohlschrauben.
S. 37 (R10/3): pmax = FMTab/Apmin *1,4
Die erhöhte Flächenpressung gilt nur, wenn jede Schraube bis über die Streckgrenze hinaus angezogen wird, mithin der Anziehdrehwinkel und das Anziehdrehmoment für jede SV unterschiedlich sein kann. Das kann für jedes Anziehverfahren gelten, nicht nur für streckgrenzen- oder drehwinkelgesteuertes. Wobei die Streuung von Zugfestigkeit und Streckgrenze bei Qualität 12.9 und 10.9 nur +15% beträgt, erst bei 8.8 und darunter +30% und mehr.
S. 37 (R12/2): FKQerf = FQmax / (qF*µTmin) + MYmax / (qM*ra*µTmin)
Die Anzahl der Trennfugen qF und qM ist eigentlich egal bei einer Einschraubenverbindung. Oder es müsste erläutert und skizziert werden, wie die Klemmteile verspannt sind.
FKQerf = FQmax/µTmin, unabhängig von der Anzahl der Trennfugen. FQ wird schließlich bei Haftreibung zu 100% auf die nächste Trennfuge übertragen.
Eher müßte bei größerem Abstand der Querkräfte durch das dadurch entstehende Biegemoment (Klaffung) die Klemmkraft noch erhöht werden.
S. 50, 51, 52
Der Biegekörper muß die tatsächlichen Abmessungen berücksichtigen (meist prismatischer Biegekörper) und kann nicht als konisch-zylindrischer Druckverformungskörper der Schraubenverbindung angenommen werden.
S. 67 Gleichung (98): phim* = n * ...
Der Krafteinleitungsfaktor für die Axialkraft FA ist hier nicht relevant.
S. 69 Tabelle 4
Zitat: "Der Abstand v ist immer positiv"
Dann muß der Abstand u auch immer positiv sein, da u + v = cT (Länge Klemmfugenfläche).
Was ist bei Wechsellast FA, z.B. Beispiel 4 (Pleuel)? Belastungsfall I im Rückhub, und Belastungsfall IV im Arbeitshub. Muß dann bei jedem Hub u und v vertauscht werden? Wieso kann nicht auch Punkt V auf der klaffgefährdeten Seite liegen? Oder kann Punkt U wahlweise Abstand u oder v zur Nullachse haben?
Die Tabelle ist überflüssig. Wenn die Schraubenachse und FA auf derselben Seite zu der Schwerpunktachse 0-0 liegen, dann ist ssym positiv, sonst negativ. Und U liegt auf der Seite von FA.
S.88, Bild 33
Im Bild fehlt eine Begrenzung durch die Zugfestigkeit (FM,Rm).
Für Schrauben 12.9 oder 10.9 wäre Rmmin < Rp0.2max.
Die in Bild 33 eingezeichnete Kurve trifft höchstens für Qualität 8.8 oder schlechter zu.
S. 88 (149)
Zitat: SigmaZ = 1/A0*(FMzul + FSAmax – delta FVth) + MSbmax/Wb
Bei exzentrischer Last fehlt die Biegespannung durch MB, und bei Betriebsbeanspruchung kann man FMzul durch FVmax ersetzen.
Zentrisch: SigmaZ = max(FMzul/A0, 1/A0*(FVmax + FSAmax – delta FVth)
Exzentrisch: SigmaZ = max(FMzul/A0, 1/A0*(FVmax – delta FVth) + SigmaSAb
Anmerkung: FSAmax/A0 sowie Msbmax/Wb ist in SigmaSab schon enthalten. Und Gleichung (186) ist zu erweitern, daß auch äußere Biegemomente MB berücksichtigt werden, siehe S.95.
S. 88: (150):
Formel (150) ist überflüssig, es gilt (149)
S 90,91: FV1
Mit der Formel für FV1 wird eine Vorspannkraft in der Verbindung nach der ersten Be- und Entlastung berechnet, welche laut (161) größer ist als die Montagevorspannkraft beim Anziehen!
S.91: (161)
Bei Zugbeanspruchung der Schraube gibt es keine Verfestigung. Höchstens durch Brucheinschnürung, was durch verminderten Querschnitt A0 kompensiert wird. Eine Werkstoffverfestigung gibt es bei Druckbeanspruchung der Klemmstücke. Diese ist bereits berücksichtigt, wenn die Grenzflächenpressung größer ist als die Zugfestigkeit.
S. 95 (186)
Biegemoment MB ist nicht berücksichtigt bei Sigma Sab.
Und die Spannung im schwächsten Querschnitt (mit A0 und Wb0 statt AS und WS) soll berechnet werden (betrifft Taillenschrauben und Hohlschrauben)
Die Formel (186) mit Biegemoment FA*a und zusätzlichem Biegemoment MB müsste lauten:
Sigma Sab = phien*FA/A0 + ßP/ßS*(FA*a – FA*ssym*phien + MB(1-sign(ssym)phim)/Wb0
S. 96 (187, 188, 189)
Die Formeln (187), (188), (189) sind überflüssig.
S.99: Gleichung (201)
C1 ist undefiniert für s/d < 1,4 sowie für s/d=1,9
S.99: Gleichung (202)
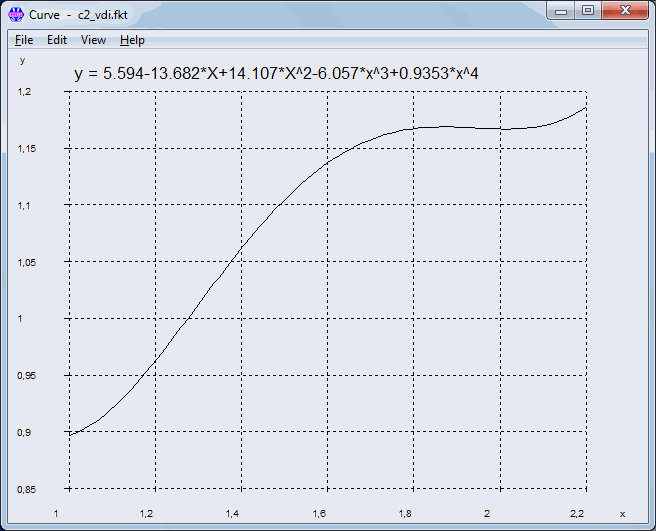
C3 = 0.728 +1.769 RS –2.896 RS^2 +1.296 RS^3
Die Funktion hat ein Maximum bei 0.429, nicht bei 0.4. Ein Minimum ist bei RS=1.061
Der Geltungsbereich sollte lauten: 0.43 .. 1
Für RS<=0.4 gilt: C3=1.055 (nicht RS=0.4).

S.102: Gleichung (211)
Polynomfunktion für Faktor C2 ist nicht stetig.
S. 103: Gleichung (217)
FQres = FQmax/qF + Mymax/(qM*ra) mit qF = Anzahl der kraftübertragenden Trennfugen
Die Querkraft nimmt zwischen den Trennfugen nicht ab, siehe auch S.37.
S. 130: Anhang B Berechnungsbeispiele:
In allen Berechnungsbeispielen wurde mit einem E-Modul der Schraube von 205000 MPa gerechnet. Der E-Modul der Schraubenwerkstoffe 8.8, 10.9 und 12.9 ist aber 210000 MPa bei 20°C. Laut Tabelle A10 (S.124) sind es sogar 211000 N/mm² für 1.551.
S. 132: Beispiel B1: R3:
Zitat: "Wegen der relativ geringen Unterschiede zwischen dem Durchmesser der Kopfauflage (dw = 17.23 mm) und dem Außendurchmesser in der Trennfuge (DSt=25 mm) ... wird vereinfacht mit mittlerem Auflagedurchmesser dwm gerechnet"
Kommentar: Der "relativ geringe Unterschied" ist "nur" 45 % (25-17,23)/17,23 * 100%.
Die genau berechnete elastische Nachgiebigkeit beträgt 0,422E-6 mm/N. Hier ist der relative Unterschied immerhin nur noch 16%.
Bei Berechnung nach VDI2230:1986 (mit Ersatzzylinder) ergibt sich deltaP = 0,39E-6 mm/N. Das ist immer noch genauer als der Verformungskegel mit mittlerem Auflagedurchmesser.
Wenn man die elastische Nachgiebigkeit als ESV berechnet, erhält man für nach VDI 2230-1:2014 deltaP = 0,304 E-6 (Fehler 38%) und nach VDI 2230:1986 deltaP= 0,39E-6 mm/N (Fehler 8%). Bei der Berechnung nach VDI 2230:1986 gibt es keinen Unterschied für ESV und DSV.
Beim Auflagedurchmesser dw der Kolbenstange ist außerdem die Fase nicht berücksichtigt, dw dürfte zwischen 23 und 24 mm liegen.
S. 136: Anhang B: Beispiel 1: R11:
TauBM/RmM=0,657, tauBS/RmS=0,62
Dann wird RS=0,985. Wenn man die Gewindetoleranzen berücksichtigt, wird RS>1 (1,01), dann ist das Außengewinde kritisch.
S. 138: Beispiel B2: R0:
Vorauslegung D: Spalte 3 von Tabelle A7 bei 100 000 N ist nicht Schraubengröße M16 sofern man die Festigkeitsklasse 10.9 wählt, sondern M18.
S. 143: Beispiel B3:
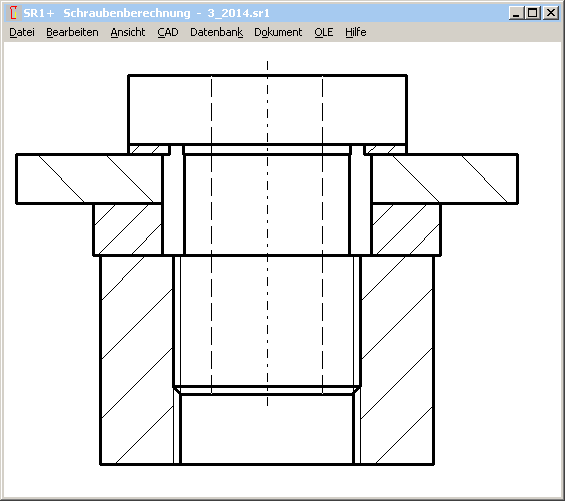
Zeichnung: Der kleinste Schraubenquerschnitt wird mit d0 berechnet. Auf der Zeichnung ist der kleinste Schaftdurchmesser der Schraube aber viel kleiner als d0. Die Scheibe hat 4mm Luft. Vielleicht ist auch nur die Bemaßung falsch, und d0 sollte der kleinste Schaftdurchmesser der Schraube sein. Und der als d0 bemaßte Absatz am Schraubenkopf d = 27mm.
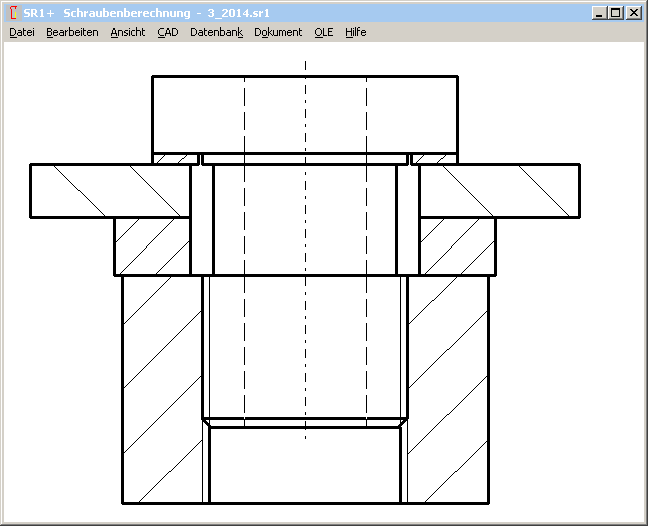
S.142,143: Anhang B, Beispiel 3:
Bei dw=36 in der Kopfauflage und dw=48 in der Mutterauflage (relativ geringer Unterschied 33%) ist die Verbindung als DSV zu berechnen (gleich wie Beispiel B1).
S.144: Anhang B, Beispiel 3:
delta i = (l1+l2+l3)/ES/(A0-ABohrung)
A0 falsch, da unterschiedliche Durchmesser für d1,d2,d3
S.145 Anhang B, Beispiel 3: Verformungskegel
Im gleichen Fall wie hier wurde in Beispiel 1 der Ersatzkegelwinkel phi als DSV berechnet, mit einem mittleren Auflagedurchmesser dwm
S.147 Anhang B: Beispiel 3: R10 Flächenpressung
Ap=pi/4*(36²-29²) = 357 mm²
pMmax = 140300N/357mm² = 393 N/mm²
Sp = 1.8
S.147 Anhang B: Beispiel 3: R10 Flächenpressung
Falsch: Tabelle A9: pG=900 N/mm²
Richtig: Tabelle A9: pG=1300 N/mm² für 16MnCr5
S.147: Anhang B: Beispiel 3: R11 Einschraubtiefe
Die verwendete Formel für RS gilt nur für gleiche Scherfestigkeitskoefizienten von Schrauben- und Mutterwerkstoff. TauBS/Rm von 8.8 ist aber 0,65 und tauBM/Rm von 16MnCr5 ist 0,85 laut Tabellen in VDI2230-1:2014. RS ist dann nicht 1,52, sondern 2,0.
Da mit dem falschen RS weitergerechnet wurde, sind die nachfolgenden Rechnungen auch falsch.
S.148: Fehler in Anhang B: Beispiel 3: R11 Einschraubtiefe
Zitat: "wobei für die Hohlschraube gilt: Rmmax*AS = FMzul"
Wie? Rmmax*AS = FMzul ? Wie geht das?
Für Hohlschrauben ist mit A0 statt AS zu rechnen, aber nicht mit FMzul.
Rmmax * A0 = 830 N/mm² * 1,2 * 251 mm² = 250 kN
Das ist fast doppelt so viel wie FM zul.
Daß als Folgefehler eine viel zu kleine Mindesteinschraubtiefe herauskommt, ist natürlich klar. Ohne den Zuschlag von 1,2*P wären es nur 4,8 mm, gerade mal zwei Gewindegänge.
Hier die richtigen Ergebnisse
meffmin = 8,0mm (statt 4,8mm) mit Rmmax*A0=250Nm und C2=1,16 aus RS=2,0
mgesmin = meffmin + mzu = 8 + 1,2*2 = 10,4 mm
Wieso ist mzu hier eigentlich 1,2*P? Bei kritischem Innengewinde ist es doch 2*P?
S. 149: Beispiel B4:
Konstruktionsfehler: Die Paßfläche der Schraube trifft nicht die Trennfläche. Entweder muß die Schraube umgekehrt (mit Schraubenkopf pleuelseitig) eingebaut werden, oder die Schraubenabmessungen sind zu ändern.
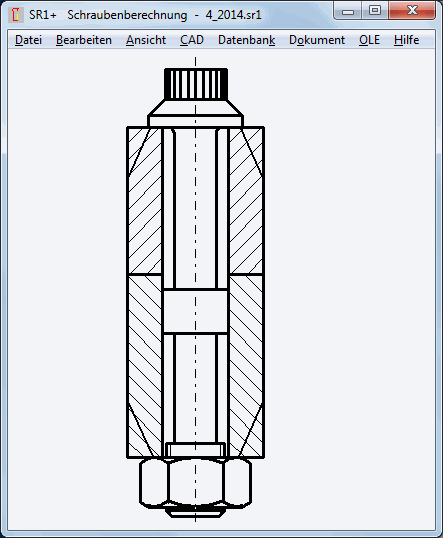
Außerdem wäre für diese Anwendung ein Feingewinde zu empfehlen.
S.149: Fehler in Anhang B: Beispiel 4: Ausgangsbedingungen
Zitat: "auf eine Zugfestigkeit von 900 N/mm² vergüteter Stahl Cq 45 gewählt"
Cq45 kann man nicht auf 900 N/mm² vergüten. +QT: 700-850 N/mm² bei t<8mm
S.150: Beispiel 4: R1 Bestimmung des Anziehfaktors alphaA
Zitat: Die Schraube wird drehwinkelgesteuert angezogen. Gemäß Tabelle A8 beträgt der Anziehfaktor alphaA=1.
Falsch: Gemäß Tabelle A8 beträgt der Anziehfaktor alphaA 1,2 bis 1,4.
alphaA=1 gibt es gar nicht. Dies ist der theoretische Idealfall ohne Streuung und Reibungstoleranzen.
S. 152: Beispiel B4: R2
Die Ermittlung der Gesamtfläche ergibt Ages = 12*25 = 300 mm², nicht 272mm².
Oder wurden hier die genauen Abmessungen verwendet? Falls ja, sollten diese auch für IBT verwendet werden, weil hier die verminderte Länge in 3. Potenz eingeht.
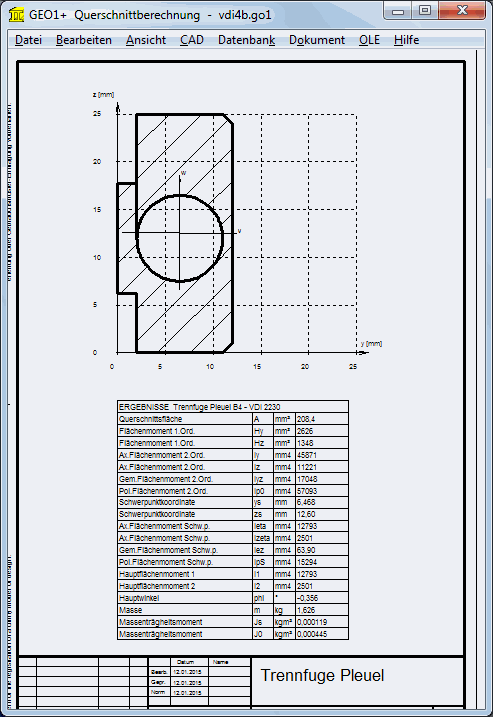
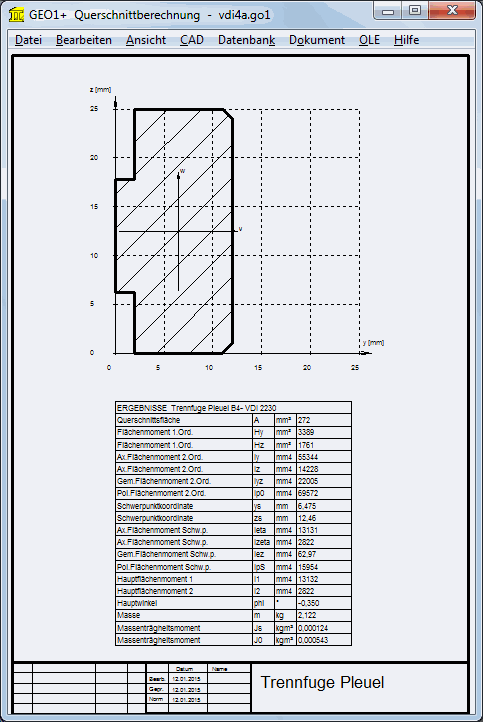
IBT = b*cT³ = 3600 mm^4
Abmessungen berechnet mit GEO1+: IBT = 2822 mm^4
S. 153: Beispiel B4, R3: Berechnung von deltaP
Die Auflagedurchmesser von Schraube und Mutter sind unterschiedlich (12,3 und 11,6mm), deshalb sind auch die Verformungskegel unterschiedlich.
deltaP= 1,407E-6 mm/N
S. 153: Beispiel B4: Biegekörper
Für die Biegenachgiebigkeit wird ein Ersatzträgheitsmoment berechnet mit einem prismatischen Biegekörper an der Trennfuge (korrekt), und anschließenden konischen Hülsen aus dem Verformungskegel (falsch). Der Querschnitt des Biegekörpers (Pleuel) ist genau umgekehrt in der Trennfuge am geringsten und wird zu Schraubenkopf und Mutter hin größer.
S.155: Beispiel 4, R8:
FV1 = 31 467 N
Dann ist die Vorspannkraft nach der ersten Belastung größer als die Montagevorspannkraft FMzul von 26 444 N! Wenn man annimmt, daß die Torsionsspannung vollständig abgebaut wurde, verbleibt Sigma0 = (FV1+FSA)/A0 = (31467N + 490N) / 26.6mm² = 1201 N/mm². Die Streckgrenze der Schraube ist aber nur 1100 N/mm²!
S.156: Beispiel 4, R8:
Zitat: Die SV genügt den Anforderungen.
Falsch: Es sollte in R8 aber nicht die Restklemmkraft, sondern die Betriebsbeanspruchung Sigma red,B ermittelt werden. Und diese genügt den Anforderungen nicht.
Da wurde wohl vergessen, die Sicherheit gegen Fließen zu berechnen.
Sigma0 = FMzul/A0 + SigmaSabmax = 26442 / 26,6 + 61 = 1055 N/mm²
taumax = MG/Wp = 363 N/mm²
Sigma red,B = 1102 N/mm² (mit ktau=0,5)
SF = Rp0,2 / Sigma red,B = 1100 / 1102 = 0,998
S. 157: Beispiel 4, R9, SigmaSAbo:
Das Biege-Widerstandsmoment im schwächsten Querschnitt muß mit dT= 5,82 mm statt mit dS = 6,827 mm und mit A0=pi/4*dT² statt AS ermittelt werden.
Dann wird Sigma SAbo = 62 N/mm²
S. 157/158: Beispiel 4, R10:
Zu Faktor 1,4 bei pmax siehe Anmerkung S. 37
Zu Grenzflächenpressung von Cq45 siehe Anmerkung S. 149
Was fehlt in Beispiel 4:
Der Arbeitshub mit Druckkraft auf das Pleuel wird nicht berücksichtigt (FAmin= -5000 N), ebenso nicht der Einfluß der erhöhten Arbeitstemperatur im Verbrennungsmotor.
S. 161: Anhang B: Beispiel 5: R2:
Zitat: Für den das Verformungsverhalten beeinflussenden Ersatzaußendurchmesser des Grundkörpers D’A,I ist der Materialbereich bis zur Zylindermitte zu beachten. Somit gilt:
D’A,I = 2*rs = DST = 175 mm
Anmerkung: Das Verformungsverhalten der Schraubenverbindung wird vom Materialbereich in Zylindermitte sicher nicht beeinflußt. Der Abstand zum Außenrand ist rx=17,5 mm und zur nächsten Schraubenbohrung ry= 14,65 mm. Dann ist "D’A,I" höchstens etwas größer als 2*rx = 35 mm.
S. 162: Anhang B: Beispiel 5:
Nachrechnung: ssym ist nicht –1,7 mm, sondern +1,98mm. Auch in Bild B7 ist ssym positiv.
Die Überprüfung der Vorzeichenregelung entspricht nicht Fall II, sondern Fall I.
Mit den Ersatz-Verformungskegeln der Schraubenverbindung kann man keine Biegung berechnen, entscheidend ist hier das Widerstandsmoment des Biegekörpers in der Trennfuge, und nicht das Flächenträgheitsmoment des Druckverformungskegels der Schraubenverbindung.
Mit GEO1+ kann man den Schwerpunkt und ssym, den "Abstand der Schraubenachse von der Achse des gedachten seitensymmetrischen Verformungskörpers" berechnen.
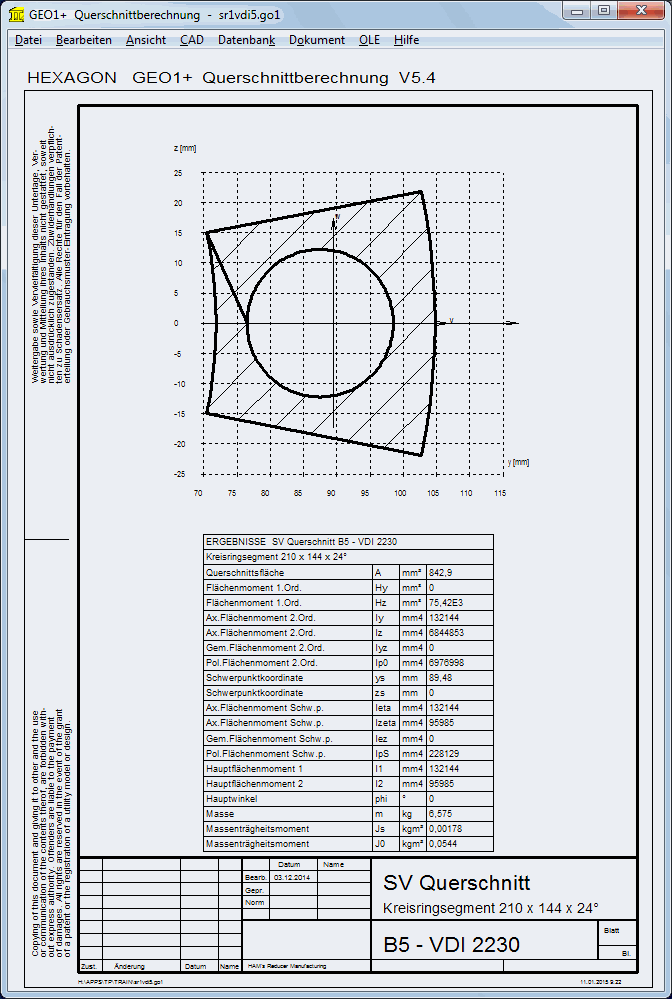
Die Koordinaten der Trennfläche wurden angegeben mit ri=72mm, re=105mm, alpha = 24°, rS=87,5mm und dh=22mm. GEO1+ berechnet ys=89,48 mm. Dann ist ssym = ys – rS = 89,48-87,5 = 1,98 mm, u = ys – ri = 89,48-72=17,48 mm und v= re - ys = 15,48 mm.
Das axiale Flächenmoment um die w-Achse ist Izeta= IBT = 95985 mm4.
S. 163
R3: deltaM ist nicht 0,104E-6, sondern 0.102E-6 mm/N
S. 164
lers = 5,93E-8*205000*pi/64*16.93^4 ergibt nicht 48,7, sondern 49,0 mm
S. 168: R8
Zitat: sigma zmax = FSmax/AS = 780,3 N/mm²
Anmerkung: Bei Sigma zmax ist die Biegespannung nicht berücksichtigt. Da diese gleich wie die Torsionsspannung in der Außenfaser ihr Maximum hat, muß sie bei der Vergleichsspannung berücksichtigt werden.
Korrekt: Sigma zmax = FMzul / As + Sigma Sab = 190000/245 + 35,6 = 811 N/mm²
Sigma red,B = 841 N/mm²
SF = 1,12
Anmerkung: Wenn man mit FVmax statt FMzul rechnet, ergibt sigma zmax = 786 N/mm²
S. 170: Beispiel B5:
R11: RS ist mit tauM/tauS statt mit RmM/RmS zu berechnen, weil tauBM/RmM=0,8 und tauBS/RmS=0,62 unterschiedlich sind. Richtig ist RS=0,79
S. 170: Beispiel B5: R11:
Die verwendete Innensechskantschraube läßt laut EN ISO 4762:2004 an der Kuppe ein unvollständiges Gewinde u <= 2P zu. Zusammen mit 1*P für das Innengewinde ist der Zuschlag zur Einschraubtiefe dann mzu = 3*P. Mit meffvorh = mvorh – 3*P = 17,5mm folgt: meffvorh < meff. Eine detaillierte Berechnung gemäß Abschnitt 5.5.5 ist damit notwendig.
Der berechnete Wert ist mit Nennmaßen für d und D2: meff = 18,2mm. Bei Berücksichtigung der Gewindetoleranzen:
6H/6h: meffmin=18,6 mm
6H/6g: meffmin=18,9 mm
6H/6e: meffmin=19,2 mm
Was fehlt in VDI 2230-1:2014 ?
Eine Tabelle der Schraubenwerkstoffe mit Zugfestigkeit, Streckgrenze, Toleranz von Streckgrenze und Zugfestigkeit, E-Modul, Scherfestigkeit, Temperaturkoeffizienten, Bruchdehnung.
05.12.2015 Fritz Ruoss