Deutsch
English
Infobrief Nr. 46 für Dezember 1997
Copyright by HEXAGON Software 1997
WL1+ Quick-Ausgabe
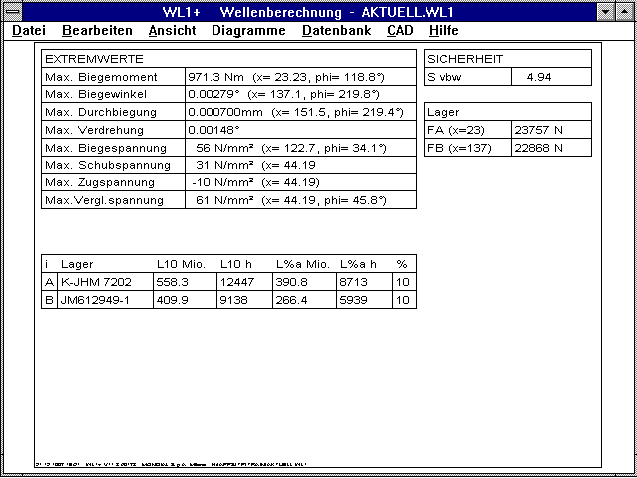
In die Quick-Ausgabe von WL1+ wurde die Lebensdauer L10 und L%a
der Wälzlager mit aufgenommen (% = Ausfallwahrscheinlichkeit in
Prozent)
WL1+ Sicherheiten
WL1+ berechnete bisher die Sicherheiten bezogen auf wechselnde
Beanspruchung von Biegung, Zug/Druck und Torsion. In der neuen
Version können Sie wählen, ob Drehmoment und Axialkräfte
wechselnd, schwellend oder ruhend auftreten.
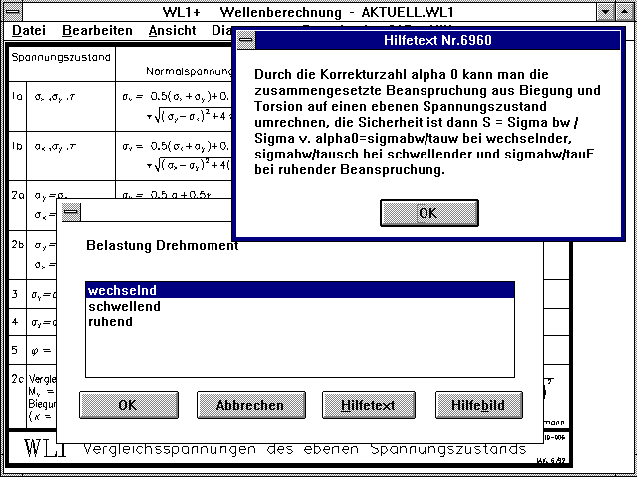In Abhängigkeit davon berechnet WL1+ dann die Vergleichsspannung
bezogen auf Sigma bw. Als Ergebnis erhält man nur noch einen Wert
für die Sicherheit:
S = Sigma bw / Sigma v.
WL1+ Belastungszustand
Für Drehmomente und Axialkräfte kann man angeben, ob die
Beanspruchung wechselnd, schwellend oder statisch sein soll.
Biegespannungen (aus Querkräften, Streckenlasten und
Biegemomenten) sind durch die Drehung der Welle immer wechselnd,
auch wenn die Belastung rein statisch ist. Die Lastfrequenz ist
gleich der Drehzahl der Welle. Anhand der Vergleichsspannung wird
der räumliche Spannungszustand auf einen ebenen Spannungszustand
umgerechnet. Die Sicherheit wird berechnet aus
S = sigma bw / Sigma v
Abhängig von der Festigkeitshypothese ist
Sigma v = SQRT ( sigma² + ( alpha0 * phi * tau )²)
Mit der Korrekturzahl alpha0 kann man die unterschiedlichen
Spannungszustände berücksichtigen:
Sigma bw
alpha0 = ------------
phi * tau
wobei für tau bei wechselndem Drehmoment tau w, bei schwellendem
Drehmoment tau sch, und bei statischer Beanspruchung tau F
eingesetzt wird. phi ist abhängig von der Festigkeitshypothese
(1,2, oder 1.73).
Beispiel: Eine Welle aus St50 ist durch das Biegemoment Mb und
das Drehmoment Mt belastet. Wie groß ist nach der Hypothese der
größten Gestaltänderungsenergie die Korrekturzahl alpha0, wenn a) die
Biegung wechselnd, die Torsion ruhend, b) beide wechselnd, c) die
Biegung ruhend, die Torsion wechselnd erfolgt ?
Aus der Werkstoffdatenbank WST1 entnimmt man die Grenzspannungen:
sigmabF=450N/mm² sigmabW=250N/mm² tauF=180N/mm² tauW=150N/mm².
Es ist also mit phi=SQRT3
a) alpha0 = sigma bW/(phi tauF) = 250 / ( SQRT3 * 180 ) = 0.8
b) alpha0 = sigma bW/(phi tauW) = 250 / ( SQRT3 * 150 ) = 0.96 ÷ 1
c) alpha0 = sigma bW/(phi tauF) = 450 / ( SQRT3 * 150 ) = 1.7
Bei WL1+ wird die Korrekturzahl alpha0 vom Programm ermittelt,
wenn man den Werkstoff aus der Datenbank wählt und die
Festigkeitskennwerte bekannt sind.
WL1+ Zug- und Biegespannung
Für die Berücksichtigung von überlagerten Zugspannungen auf die
Vergleichsspannung wird die Zugspannung auf den
Biegewechselspannungsanteil der Vergleichsspannung folgendermaßen
umgerechnet:
sigmaz wechselnd: sigmavb = sigmab + sigmaz * sigmabw / sigmaw
sigmaz schwellend: sigmavb = sigmab + sigmaz * sigmabw / sigmasch
sigmaz ruhend: sigmavb = sigmab + sigmaz * sigmabw / Re
WL1+ Krit.Drehzahl für 3-fach Lagerung
Auch für 3-fach gelagerte Wellen kann man nun die
Resonanzdrehzahl für Biegeschwingungen berechnen. Da hierdurch
die Rechenzeit um ein mehrfaches erhöht wird, kann man nun unter
"Bearbeiten->Berechnung" die Berechnung der biegekritischen
Drehzahl abschalten. Die Kritische Drehzahl für Drehschwingungen
ist unabhängig von der Anzahl der Lagerstellen, und kann daher
immer ausgegeben werden.
FED8 - Federarbeit
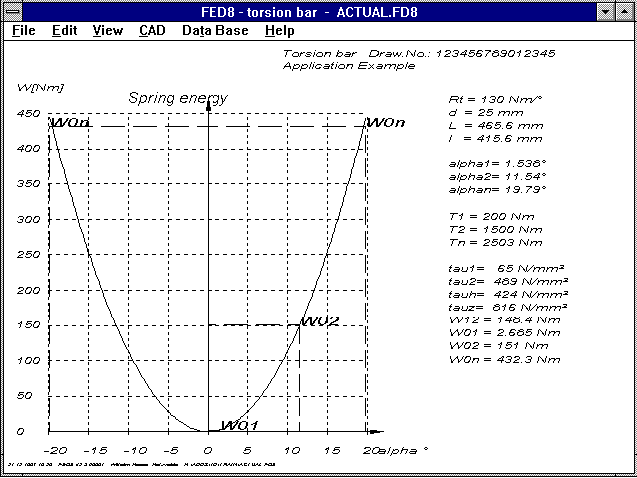Ein Diagramm mit dem Verlauf der Federarbeit wurde in die
FED8-Software zur Berechnung von Drehstabfedern aufgenommen. Bei
wechselnd beanspruchten Drehstabfedern geht der Verdrehwinkel von
-alpha bis +alpha. Die maximale Federarbeit von -alphan .. +alphan ist
dann Mn * alphan (Index n=nutzbarer Verdrehwinkel für Schubspannung
tau n = tau zul).
FED2 - Oberspannung und tau zul
Theoretisch müßten die zulässige Schubspannung für statische
Beanspruchung und die Oberspannung im Goodman-Diagramm identisch
sein. Normalerweise trifft dies auch zu, bei manchen Werkstoffen
gibt es jedoch Abweichung bis ca. 15%. Das kommt davon, daß für
die Berechnung von tau zul und für die Herleitung der
Goodman-Diagramme unterschiedliche Quellen verwendet wurden. Die
Goodman-Diagramme stammen aus DIN 2089, die Zugfestigkeitswerte
aus der EN 10270, welche der alten DIN 17223 entspricht. Bei der
Druckfederberechnung ist tau zul = 0.56 * Rm (nach DIN 2089). Bei
der Zugfederberechnung wird laut DIN 2089 Blatt 2 die zulässige
Schubspannung als 0.45 * Rm eingesetzt. Das Goodman-Diagramm ist
jedoch dasselbe für Druck- und Zugfeder, deshalb ergeben sich bei
der Zugfeder größere Abweichungen. Ausschlaggebend für die
Dauerfestigkeit von Zugfedern mit Ösen ist jedoch fast immer die
Biegespannung im Ösenübergang. Durch Verwendung von eingerollten
oder eingeschraubten Ösen oder Gewindebolzen kann diese
Schwachstelle eliminiert werden.
FED2 - Index kn
Bei der Zugfederberechnung wird der Index n als nutzbarer
Federweg für statische Beanspruchung ausgegeben, bei dem die
Schubspannung tau n = tau zul ist. Bei dynamischer Beanspruchung
werden für tau k1 und tau k2 die korrigierten Schubspannungen
(tau k = tau * k) eingesetzt, bei statischer Beanspruchung wird
der Spannungskorrekturfaktor k nicht berücksichtigt (entsprechend
DIN 2089). Im Auszug werden für Pos. 1 und 2 die korrigierten
Schubspannungen tau k1 und tau k2 eingesetzt, für Pos. 0 und n
dagegen die statischen Werte tau 0 und tau n. In der neuen
Version wird tau kn = tau n * k zusätzlich ausgegeben, und der
zugehörige maximale Federweg bei dynamischer Beanspruchung
berechnet. Dadurch wird klarer, wieso tau k2 größer als tau n
sein kann.
======================================================================
Federlänge mm Federweg mm Federkraft N tau N/mm² S
======================================================================
L0= 27.47ñ0.8 F0= 8.47 tau0 = 86
L1= 39.98 s1= 12.51 F1= 45.62ñ5.38 tauk1= 559 1.39
sh= 10.00 Fh= 29.69 taukh= 364 1.09
L2= 49.98 s2= 22.51 F2= 75.31ñ5.83 tauk2= 923 0.84
Lkn= 45.96 skn= 18.49 Fkn= 63.38 taukn= 777 1.00
Ln= 50.41 sn= 22.94 Fn= 76.58 taun = 777 1.00
----------------------------------------------------------------------
(S = tau zul. / tau y)
Sigma zul. / Sigma q2 = 0.68 Sigma hzul. / Sigma bh = 0.67
In diesem Beispiel einer dynamisch beanspruchten Zugfeder ist tauk2
größer als taun, obwohl der Federweg s2 kleiner als sn ist. Jedoch
ist der Federweg s2 größer als der bei dynamisch beanspruchter
Feder nutzbare Weg skn. Bei Zugfedern mit Öse besteht die größte
Ausfallgefahr meist im Ösenübergang, wenn die zulässige
Biegespannung überschritten wird. Auch in diesem Beispiel wird
die Zugfeder am Ösenübergang brechen, bevor die zulässige
Schubspannung in den Windungen überschritten wird, da die
zulässige Biegespannung Sigma zul. im Ösenübergang weit vor der
zulässigen Schubspannung überschritten wird.
FED2 - Vorspannkraft
Wenn nur eine Federlänge und eine zugehörige Federkraft
vorgegeben ist, gibt man bei der Druckfederberechnung F1=0 und
L1=L0 und sh=s2 ein. Bei der Zugfederberechnung ist das anders,
da zuerst die Vorspannkraft überwunden werden muß, mit der die
Windungen aneinanderliegen. Man darf also bei der Auslegung und
Vorauslegung nicht F1=0 eingeben, sondern muß für F1 die
Vorspannkraft F0 einsetzen.
10 Jahre HEXAGON-Software
Die HEXAGON GmbH gibt es zwar erst seit 1990, bereits 1987 wurde
jedoch die erste Software, das Toleranzprogramm TOL1 entwickelt.
Parallel zum Informatik-Aufbaustudium wurden im Ingenieurbüro
Ruoss Programme für den Konstrukteur im Maschinenbau geschrieben,
auf einem 8086-PC mit 4,77 MHz Taktfrequenz und 256 kB Speicher,
360 kB Diskettenlaufwerk, ohne Festplatte (Das war schon ein
gewaltiger Fortschritt gegenüber dem Vorgängerrechner, einem
Sinclair ZX81 mit nur 1 kB Speicher!).
Das Entwicklungswerkzeug Turbo Pascal 3.0 enthielt in einer nur
40 kB großen Datei (TURBO.COM) Compiler und Programmeditor. So
fanden auf einer einzigen 360 kB-Diskette Entwicklungswerkzeug,
Quelltexte und fertige Programme Platz. Zum Vergleich: Borland
Delphi 3.0, der Nachfolger von Turbo Pascal, benötigt ca. 100 MB
Speicherplatz auf der Festplatte, das ist eine Steigerung um den
Faktor 2500 ! Nach dem Toleranzprogramm TOL1 kam das
Zahnradprogramm ZAR1 und das Druckfederprogramm FED1. Highlight
bei den Programmen war die graphische Darstellung der Zahnform
bei ZAR1 und die Federzeichnung bei FED1, später die
CAD-Schnittstelle mit Ausgabemöglichkeit als DXF- und IGES-Datei.
Eine CAD-Schnittstelle bei Berechnungsprogrammen war damals neu,
das gab es nur bei HEXAGON-Software. Während die meisten Anwender
damals wenig Wert auf die CAD-Schnittstelle legten, gehört eine
solche heute heute zu den Grundanforderungen an ein
Berechnungsprogramm. Bei Datenbanken für Werkstoffkennwerte und
Normteile wird bis heute das Ur-DBF-Format von dBase 3+
verwendet, dadurch können die Dateien alternativ mit jedem
Datenbank- oder Tabellenkalkulationsprogramm (dBase, Access,
FoxPro, Excel, Quattro Pro, StarOffice) bearbeitet werden. Nach
Toleranzprogramm, Zahnradprogramm und Druckfederprogramm
enstanden die beiden Grafik-Konvertierungsprogramme HPGL-Manager
und DXF-Manager, welche auch für die interne Programmentwicklung
gute Dienste leisten (Generierung von Quellcode für die
Grafikprogrammierung aus DXF-Zeichnungen). Dann kamen die
Programme zur Zug- und Schenkelfederberechnung, Wellenberechnung,
Schraubenverbindungen, Preßpassungen und Welle-Nabe-Verbindungen.
Daneben wurde auch ständig an der Verbesserung der Oberfläche
gearbeitet.
Seit 1992 gibt es eine UNIX-Version vom HPGL-Manager und ZARXE,
für Workstation von DEC und SUN. Obwohl 1990-92 viel nach
Unix-Versionen gefragt wurde, wollte sie nach Verfügbarkeit
keiner mehr haben, so daß die Weiterentwicklung auf Unix-Ebene
eingestellt wurde. Weit erfolgreicher war dagegen die Portierung
auf Windows. Im Juni 1993 gab es den HPGL-Manager für Windows.
Nach und nach wurden alle Programme auf Windows portiert, und
heute werden zu 95% Windows-Versionen bestellt.
Rückschau und Ausblick
1997 war für HEXAGON ein sehr erfolgreiches Jahr. Besonders aus
dem Ausland gab es enorme Steigerungen, der Exportanteil am
Umsatz stieg auf über 50%. Viele Programme gingen in das
europäische Ausland und in die USA. Auch von Argentinien,
Australien, Brasilien, Korea, Taiwan, Mexiko, Indien, Israel
wurde HEXAGON-Software geordert. Von der SR1-Software zur
Schraubenberechnung nach VDI 2230 wurden 1997 mehr Programme in
den USA verkauft als in Europa, Caterpillar hat soeben seine
dritte SR1-Lizenz erworben.
Von Januar bis Mitte Dezember 1997 gab es 689 neue Installationen
von HEXAGON-Software. Meistverkauft war HPGLVIEW mit 129
Installationen. Das jedoch nur, weil eine Firma zunächst 20
Lizenzen, und nach erfolgreicher Einführung weitere 100 Lizenzen
gekauft hatte. Kurios: Ohne diese 120 Lizenzen wäre HPGLVIEW das
Programm mit den schlechtesten Verkaufszahlen ! 73 neue
Installationen gab es von FED1/FED1+/FED1-, gefolgt von DXFPLOT
(53), FED2/FED2+ (49), FED3/FED3+ (42) und FED7 (42), ZAR1/ZAR1+
(36), FED5 (33), SR1 (30), WL1/WL1+ (24), HPGLMAN (19). Insgesamt
am meisten Installationen gibt es von FED1/FED1+ (422), gefolgt
von ZAR1/ZAR1+ (268), TOL1 (247), FED2/FED2+ (214), FED3/FED3+
(193), WL1/WL1+ (174). Mit mehr als 3200 Installationen
(weltweit) ist HEXAGON Marktführer für
Maschinenelemente-Berechnungsprogramme.
1997 gab es als neue Programme TOL2 und TOL1CON zur
Toleranzrechnung in Verbindung mit TOL1, sowie TR1 zur
Trägerberechnung. Neu bei allen Programmen ist, daß man,
alternativ zum Ergebnisausdruck auf Drucker, eine mit Netscape
oder Internet Explorer lesbare HTML-Datei erzeugen kann. Für 1998
sind mehrere Neu- und Weiterentwicklungen geplant.
Mehrsprachige Updates
Alle HEXAGON-Programme gibt es auch als englische Version. Wenn
Sie die Programmausdrucke auch in englisch oder in einer anderen
Sprache benötigen, können Sie von Ihrer Lizenz zum Preis von 90
DM eine fremdsprachige Version bestellen, wenn diese auf dem
gleichen Rechner installiert wird. Die Eingabedateien sind
kompatibel, Sie können vorhandene Berechnungsdateien mit dem
gleichen Programm egal welcher Sprache öffnen. Wenn Sie mit einer
älteren Version arbeiten, sollten Sie ein Disk-Update für 60 DM
oder ein Voll-Update für 100 DM gleich mitbestellen, daß alles
auf dem neuesten Stand ist.
Maschinenbaupaket und Komplettpaket
In das HEXAGON-Maschinenbaupaket wurden die Programme TOL2 und
TOL1CON aufgenommen, GEO1 wird durch GEO1+ ersetzt. Der neue
Preis für das HEXAGON-Maschinenbaupaket beträgt beträgt DM
13.850. Das HEXAGON-Komplettpaket wurde um TOL2, TOL1CON, TR1 und
FED8 erweitert, GEO1 wird durch GEO1+ ersetzt, der Preis erhöht
sich dadurch auf DM 18.500.
WN2 - Fußhöhe
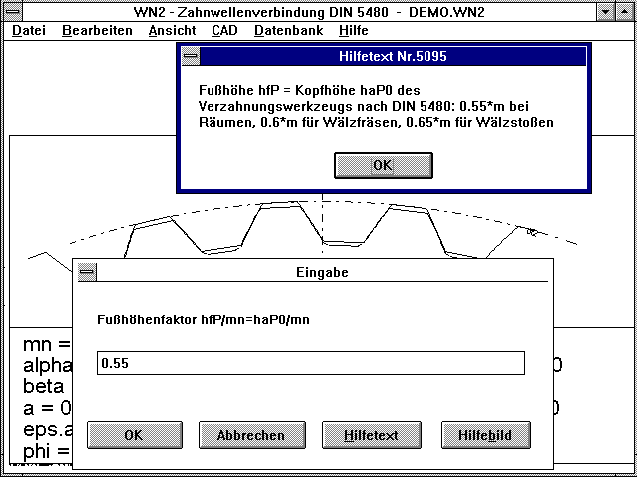Die Zahn-Fußhöhe hfP bzw. Werkzeug-Kopfhöhe haP0 war bisher auf
0.55*m fest eingestellt, nach DIN 5480 wird dieser Faktor bei
Herstellung der Verzahnung durch Räumen verwendet. Für die
Herstellung durch Wälzfräsen wird jedoch ein Faktor von 0.6*m,
und für Wälzstoßen ein Faktor von 0.65*m empfohlen. Mit der neuen
Version von WN2 kann man nun den Fußhöhenfaktor frei eingeben.
Für den Hinweis bedanke ich mich bei Herrn Canovas von Moog,
Böblingen.
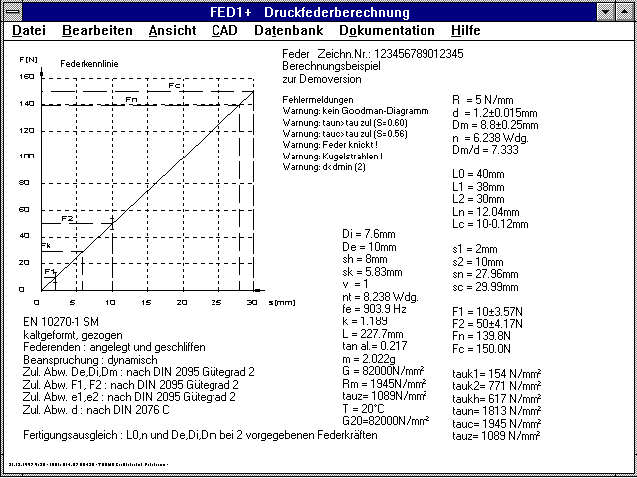
FED1+ Quick-Ausgabe
Die Ausgabe des Fertigungsausgleichs wurde um 1 Zeile nach unten
verschoben. Dadurch wird vermieden, daß der Text in der 2. Spalte
überschrieben werden kann.
FED3+ Einspannwinkel
Bei der Drehfeder läuft der Einspannwinkel delta entgegengesetzt
zum Federwinkel alpha. Dies wird oft mißverstanden, und war auch
in dem Hilfebild zum Anwendungsbeispiel falsch eingezeichnet.
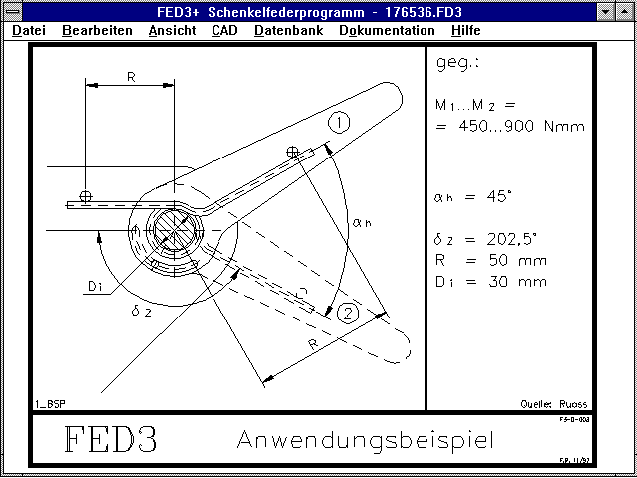Analog zur Druckfeder mit: L = L0 - s
gilt für die Schenkelfeder: delta = delta0 - alpha
FED3+ Einspannung
Im Programm kann zwischen fester Einspannung und abgestütztem
Schenkel gewählt werden. Bei abgestützem Schenkel wird zusätzlich
der Hebelarm zur Mittelachse abgefragt, das Programm berechnet
dann die Durchbiegung des Schenkels und daraus die zusätzliche
Verdrehung ß. Bei fest eingespanntem Schenkel wird die Feder
direkt am Außendurchmesser gehalten. Wenn die Federenden axial
abgebogen oder nach innen gebogen sind, ist ebenfalls "feste
Einspannung" zu wählen. Die Hilfetexte wurden entsprechend
erweitert.
Windows-Versionen für NT
Alle Windows-Versionen seit 1996 können Sie problemlos auch unter
Windows NT installieren. Die einzige Einschränkung ist, das Sie
für Dateinamen weiterhin das 8.3 Format mit max. 8 Zeichen und 3
Zeichen für Erweiterung verwenden müssen.
Dateiname: Keine Leerzeichen verwenden !
Verwenden Sie in Dateinamen bitte keine Leerzeichen, obwohl dies
mit Windows 95/NT und den alten DOS-Versionen möglich ist. Es
könnte sonst sein, daß Sie beim Wechsel auf eine neuere Version
Ihre alten Dateien nicht mehr laden können. Wenn dieser Fall
bereits aufgetreten ist, bleibt nichts anderes übrig, als die
alte DOS-Version nochmals zu installieren, alle Dateien mit
Leerzeichen laden und mit anderem Namen ohne Leerzeichen
speichern.
Seminarplan 1998
Im Früjahr und Herbst 1998 finden wieder Seminare zu Zahnrad- und
Getriebeberechnung, Federberechnung,
Betriebsfestigkeitsberechnung und Zertifizierung nach DIN ISO
9001 statt Neu aufgenommen wurde das Thema "Schwingungs- und
Geräuschverhalten von Getrieben" von Dr. Müller, mit dem immer
wichtiger werdenden Thema zur Geräuschminimierung von Getrieben.
Seminar Zahnrad- und Getriebeberechnung (2-tägig)
Dozent: Körner
Termine: 18.-19.03.1998, 14.-15.10.1998
Kursgebühr: 1000,- DM
Schwingungs- und Geräuschverhalten von Getrieben (1-tägig)
Dozent: Müller
Termine: 20.03.1998, 16.10.1998
Kursgebühr: 500,- DM
Betriebsfeste Dimensionierung von Bauteilen (1-tägig)
Dozent: Zammert
Termin: 16.03.1998
Kursgebühr: 500,- DM
Federberechnung (1-tägig)
Dozenten: Schnitzer, Zammert
Termine: 17.03.1998 und 20.10.1998
Kursgebühr: 500,- DM
Zertifizierung nach DIN ISO 9001 (1-tägig)
Dozent: Körner
Termin: 13.10.1998
Kursgebühr: 400,- DM
Zeitplan
Kursdauer: 8.45 - 16.15Uhr
Kaffeepause 10.15 - 10.30 Uhr
Mittagspause 12.00 - 13.00
Dozenten
Tillmann Körner, Dr.-Ing., VOITH TURBO Antriebstechnik
Wolf-Udo Zammert, Prof.Dr.-Ing., FHT Esslingen/Göppingen
Jürgen Schnitzer, G.S. Technik, Meinerzhagen
Robert Müller, Dr.-Ing., VOITH TURBO Antriebstechnik
Ausstattung
Die maximale Teilnehmerzahl ist auf 5-6 begrenzt. Jedem
Teilnehmer steht ein PC zur Verfügung. Softwareseitig kann mit
allen HEXAGON-Programmen gearbeitet werden. Jeder Teilnehmer
erhält einen Ordner mit Schulungsunterlagen.
Kursgebühr
Die angegebenen Kursgebühren verstehen sich zuzügl. 15%
MwSt. Mit enthalten sind Seminarunterlagen, Pausengetränke
und Mittagessen.
Seminar 1: Zahnrad- und Getriebeberechnung
- Auslegung einer Kfz-Getriebe-Vorgelegewelle mit angeschlossenem
Hydrostat mit den Programmen ZAR1+, WL1+ (Wellen- und
Wälzlagerberechnung), WN1 (Preßpassungen) und TOL1
(Toleranzrechnung).
Aufgabenstellung, Abschätzung, Vorauslegung mit ZAR1,
Geometrieberechnung, Graphische Darstellung der Zahnform,
Festigkeitsberechnung nach DIN 3990, Definition einer
Getriebewelle (Abmessungen), Übernahme der Zahnkräfte in WL1,
Wellenberechnung mit WL1, Prüfung der Welle auf max. Spannungen,
Durchbiegung, kritische Drehzahlen, Optimierung der Welle,
Auswahl und Berechnung der Wälzlager mit WL1+, Toleranzrechnung
mit TOL1.
Optimierung von Zahnrädern und Getrieben durch Variation von
Profilverschiebungsfaktor und Zahnform, Vorgehensweise bei
Optimierung für hohe Tragfähigkeit, ausgeglichenes spezifisches
Gleiten, hohe Förderleistung bei Pumpenzahnrädern
- Hohlräder, Planetengetriebe, Kegelradgetriebe.
Seminar 2: Schwingungs- und Geräuschverhalten von Getrieben
Dieses Seminar ist gedacht als sinnvolle Ergänzung, um neueste
Erkenntnisse zu Fragen der Geräuschanregung von Verzahnungen und
zum Geräuschverhalten von Getrieben kennenzulernen und diese
Ergebnisse bereits bei der Verzahnungsauslegung mit
berücksichtigen zu können. Im einzelnen werden folgende Themen
behandelt:
- Grundlagen zur Schwingungsanregung und zum
Schwingungsverhalten
- Dynamisches Verhalten von Zahnradgetrieben; Bestimmung der
Bezugsdrehzahl N sowie des Dynamikfaktors Kv.
- Schwingungsverhalten des Getriebes insgesamt: Einfluß des
Gesamtsystems "Getriebe" einschließlich Antriebs- und
Arbeitsmaschine, auch unter Berücksichtigung z.B. der
Wellenbiegung.
- Maßnahmen zur Beeinflußung der Schwingungs- und
Geräuschanregung bei Stirnradgetrieben; Verzahnungsgeometrie,
Verzahnungsabweichungen und Verzahnungskorrekturen,
Zahnflankenspiel, etc.
- Einflußparameter bei Kegelrad getrieben
- Besondere Schwingungserscheinungen: Getrieberasseln
- Zusammenhang zwischen der Geräuschanregung und der
Schallabstrahlung eines Getriebes.
- Maßnahmen zur Beeinflussung von Körperschalleitung und
Geräuschabstrahlung: Gehäusegestaltung
- Ausgewählte Fragen zur Meßtechnik
Seminar 3: Federberechnung
Berechnungsgrundlagen Druck-, Zug-, Schenkel-, Teller-,
Kegelfedern, Federkennlinien, Parallel- und Reihenschaltung von
Federn, Berechnung von Federn mit nichtlinearer Kennlinie,
Dauerfestigkeitsschaubild (Goodman-Diagramm),
Fertigungstoleranzen und statistische Ausschußbestimmung,
Optimierung und Kosteneinsparungsmöglichkeiten, Kugelstrahlen und
Warmsetzen, Anwendungsbeispiele mit den Programmen FED1-FED7,
Ausgabe von Diagrammen und Zeichnungen auf Drucker und Plotter,
Prüfen von Federn, Qualitätskontrolle.
Homepage